同步互斥

发表于 分类于

进程并发执行可提高程序效率，但是并发执行过程是不确定性和不可重现的。在进程间有共享资源，而处理过程并不是整体执行，所以会存在和预期不一致的问题。借助生活中同步问题例子，我们设计了一系列方案并进行改进。

背景

并发进程的正确性

程序正确性

程序执行的结果是实现预期的功能，并且是确定的和可重现的

并发进程执行过程是不确定性和不可重现的，程序错误可能是间歇性发生的

  • 独立进程
    • 不和其他进程共享资源或状态
    • 确定性 输入状态决定结果
    • 可重现 能够重现起始条件
    • 调度顺序不重要
  • 并发进程
    • 在多个进程间有资源共享
    • 不确定性
    • 不可重现

进程并发执行的优点

进程需要与计算机中其他进程或设备进行协作

共享资源

  • 多个用户共用一台计算机

加速

  • I/O操作和CPU计算可以并行
  • 程序可划分成多个模块放在多个处理机上并行执行

模块化

  • 将大程序分解成小程序，使系统易于复用和扩展

并发执行的问题

以并发执行创建新进程时的标识分配为例子，

调用函数fork()来创建一个新的进程（操作系统需要分配一个新的并且唯一的进程ID）

在内核中，这个系统调用会执行

1
new_pid = next_pid++

假定next_pid为100

预期结果

  • 一个进程ID为100
  • 另一个进程ID为101
  • next_pid应该增加到102

实际可能结果

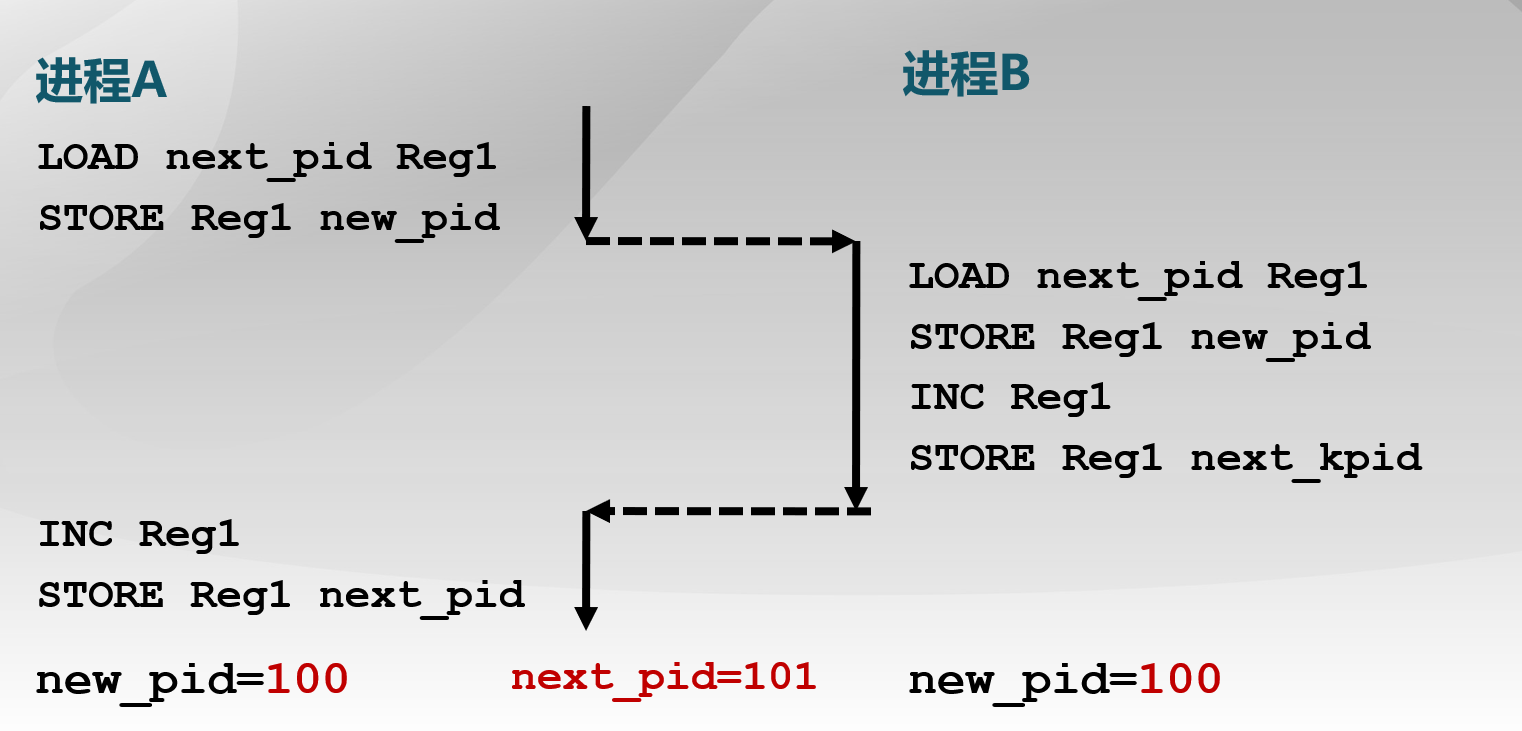
进程A和进程B的寄存器相互独立，失败原因：二者处理过程并不是整体执行

原子操作(Atomic Operation)

一次不存在任何中断或失败的操作

  • 要么操作成功完成
  • 要么操作没有执行

不存在部分执行的状态

操作系统需要利用同步机制在并发执行的同时，保证一些操作是原子操作

同步问题

现实生活中的同步问题

时间 A B
3：00 查看冰箱，没有面包了
3：05 离开家去商店
3：10 到达商店 查看冰箱，没有面包了
3：15 购买面包 离开家去商店
3：20 到家，把面包放进冰箱 到达商店
3：25 购买面包
3：30 到家，把面包放进冰箱

家庭采购问题的分析

  • 有人去买面包
  • 最多只有一个人买

可能的解决办法：

  • 在冰箱上设置一个钥匙
  • 去买面包之前锁住冰箱并且拿走钥匙

加锁导致的问题

冰箱中还有其他食物时，别人无法取到

方案一

使用便签来避免购买太多面包

1
2
3
4
5
6
7
if(noBread) {
  if(noNote) {
    leave Note;
    buy bread;
    removen Note;
  }
}

解决方案只是间歇性的失败

问题难以调试，生活中不会出现(无法察觉他人正在检查便签)

必须考虑调度器所做的事情

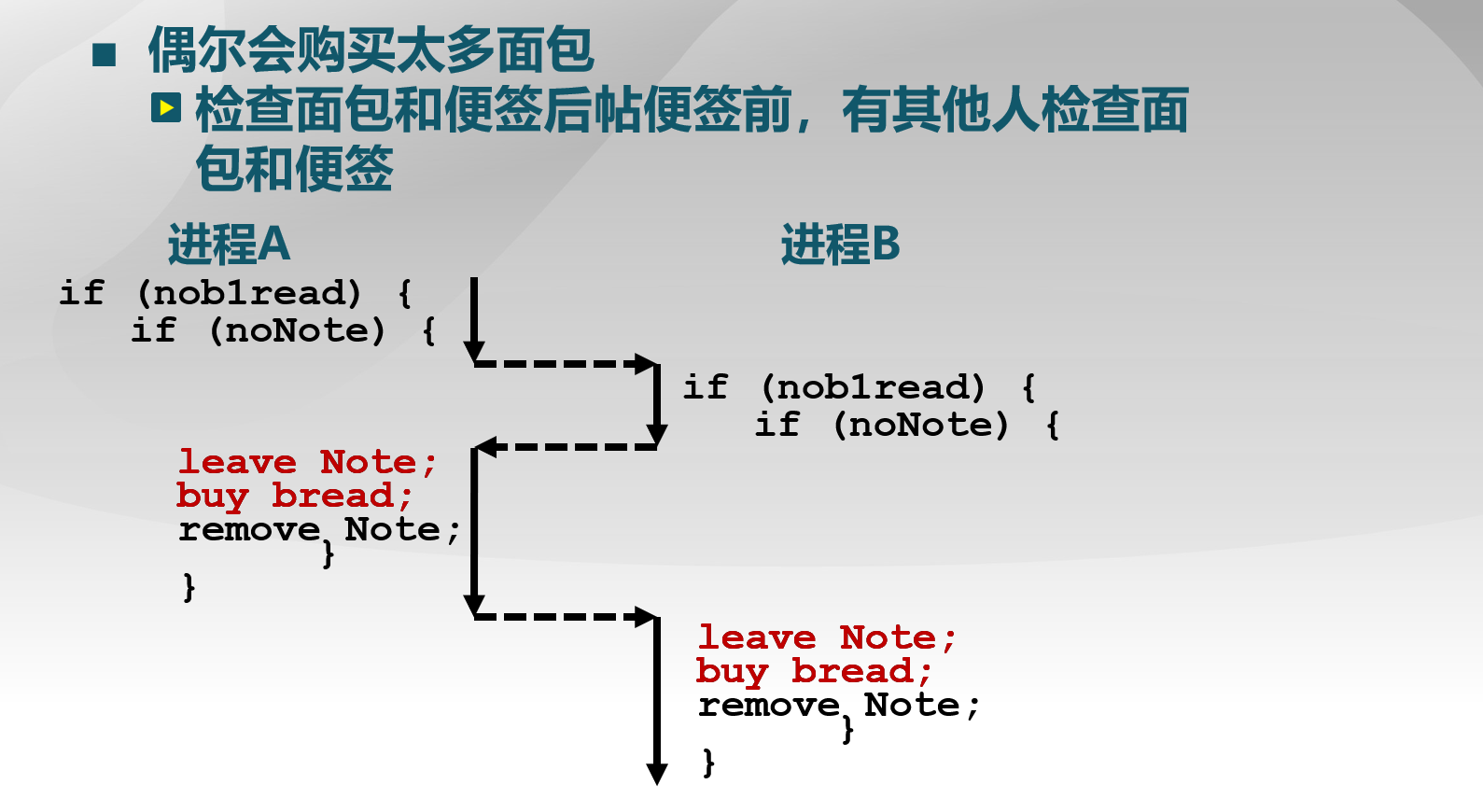
进程A和进程B均检测到没有便签，都留下便签然后去买面包

方案二

先留便签，后检查面包和便签

1
2
3
4
5
6
7
leave Note;
if(noBread) {
  if(noNote) {
    buy bread;
  }
}
remove bread;

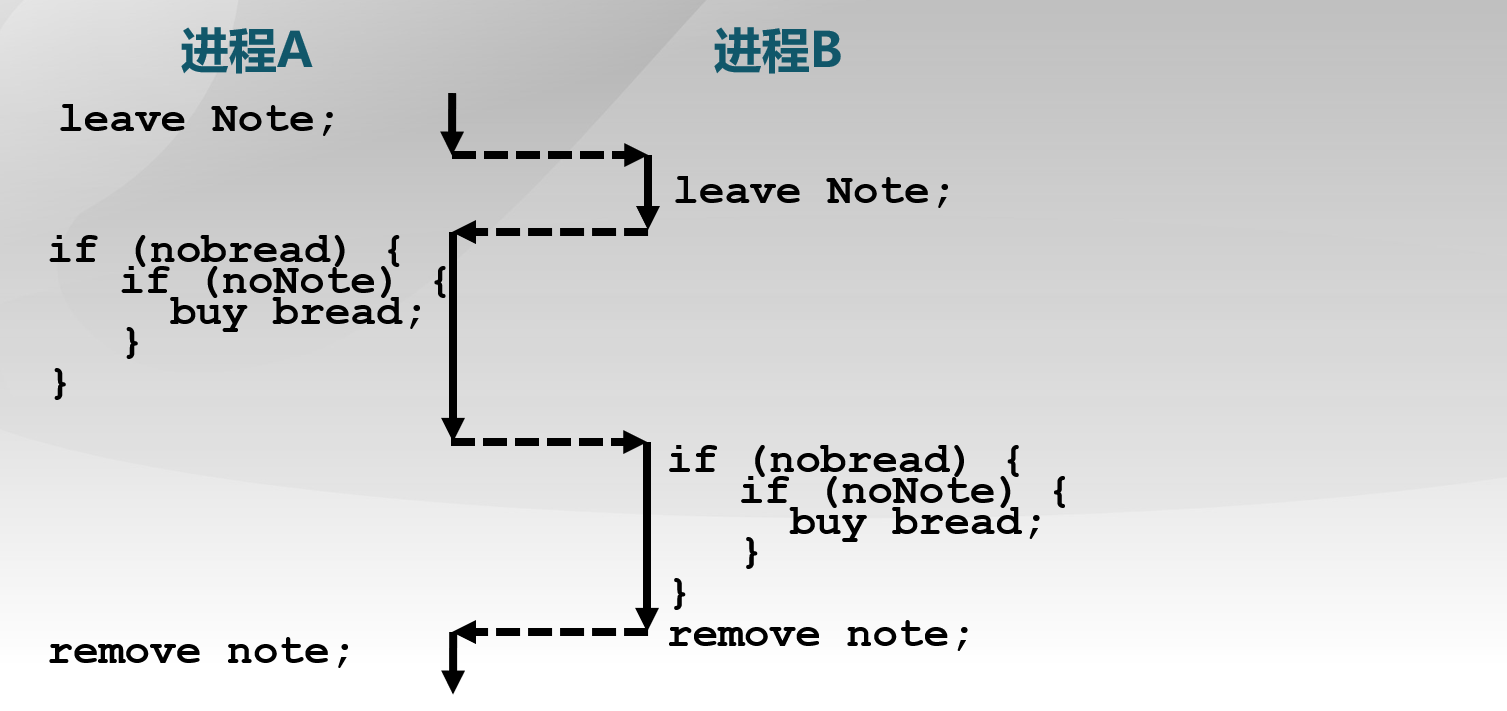
进程A和进程B二者均留下便签，然而谁也不会去买面包

此时需要提及的一点是，方案二单进程运行也买不了面包，在检测标签的时候会检测到自己留下的标签，不会去买面包。

方案三

为便签增加标记，以区别不同人的便签，可在检查之前留便签

进程A

1
2
3
4
5
6
7
leave note_1;
if (no note_2) {
   if (no bread) { 
     buy bread; 
   } 
} 
remove note_1;

进程B

1
2
3
4
5
6
7
leave note_2;
if (no note_1) {
   if (no bread) { 
     buy bread; 
   } 
} 
remove note_2;

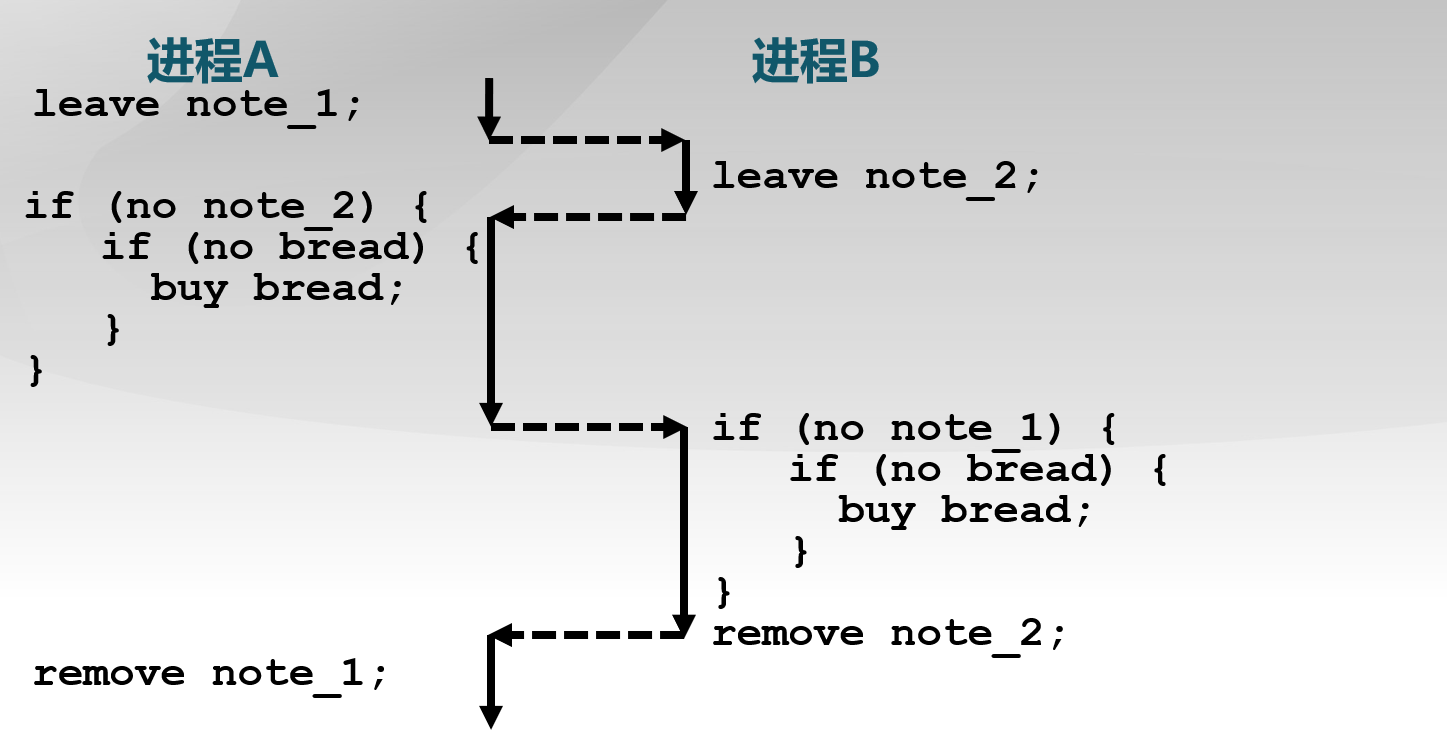
  • 二者均不会检查是否有面包，导致没有人去买面包
  • 每个人检测到对方留下的便签以后都认为另外一个去买面包

方案四

两者采用不同的处理流程

进程A

1
2
3
4
5
6
7
8
leave note_1;
while(note_2) {
   do nothing;
} 
if(no bread){
  buy bread;
}
remove note_1;

如果没有便签2,那么A可以去买面包，否则循环等待B直到离开

进程B

1
2
3
4
5
6
7
leave note_2;
if(no note_1) {
   if(no bread){
      buy bread; 
   } 
}
remove note_2;

如果没有便签1,那么B可以去买面包，否则B离开并且再试一次。

枚举所有可能后，可能确认有效。

分析

  • 它有效，但太复杂，难以验证有效性
  • A和B代码不同，每个进程的代码略有不同，更多进程的情况更为复杂
  • 当A在等待时，它不能做其他事，这称为忙等待（busy-waiting）

方案五

利用两个原子操作实现一个锁（lock），处理过程不会被打断

Lock.Acquire()

  • 在锁被释放前一直等待，然后获得锁
  • 如果两个线程都在等待同一个锁，并且同时发现锁被释放了，那么只有一个能够获得锁

Lock.Release()

  • 解锁并唤醒任何等待中的进程
1
2
3
4
5
breadlock.Acquire(); // 进入临界区
if(noBread) {
  buy bread;
}
breadlock.Release(); // 退出临界区

进程的交叉关系

相互感知的程序 交互关系 进程间的影响
相互不感知(完全不了解其他进程的存在) 独立 一个进程的操作对其他进程的结果无影响
间接感知(双方都与第三方交互，如共享资源) 通过共享进行协作 一个进程的结果依赖于共享资源的状态
直接感知(双方直接交互，如通信) 通过通信进行协作 一个进程的结果依赖于从其他进程获得的信息

关系：

  1. 互斥（mutual exclusion）一个进程占用资源，其他进程不能使用
  2. 死锁（deadlock）多个进程占用部分资源，形成循环等待
  3. 饥饿（starvation） 其他进程可能轮流占用资源，一个进程一直得不到资源

临界区

进程中访问临界资源的一段需要互斥执行的代码

1
2
3
4
entry section
  critical section
exit section
  remainder section

访问规则：(互斥访问)

  • 空闲则入
  • 忙则等待 有进程在临界区时，其他进程均不能进入临界区
  • 有限等待 等待进入临界区的进程不能无限期等待(对等待时间有约定)
  • 让权等待（可选） 不能进入临界区的进程，应释放CPU（如转换到阻塞状态）

实现方法：

  1. 禁用中断 无法响应中断
  2. 软件方法 共享变量协调，复杂
  3. 更高级的抽象方法 借用操作系统服务来提供同步的服务(引入管理者)

禁用硬件中断同步方法

没有中断，没有上下文切换，因此没有并发

  • 硬件将中断处理延迟到中断被启用之后
  • 现代计算机体系结构都提供指令来实现禁用中断
1
2
3
local_irq_save(unsigned long flags);
critical section
local_irq_restore(unsigned long flags);

进入临界区：禁止所有中断，并保存标志
离开临界区：使能所有中断，并恢复标志

缺点：

  • 禁用中断后，进程无法被停止
  • 可能导致其他进程没有执行机会，处于饥饿
  • 临界区可能很长 无法确定响应中断的时间(可能存在硬件影响)
  • 不得不用时使用

基于软件的同步方法

两个线程，T0和T1

线程Ti的代码：

1
2
3
4
5
6
do {
  enter section // 进入区
    critica sectio
  exit section //退出区
    remainder section
}while(1);

在进入区和退出区对变量修改来同步他们之间的行为。

线程可通过共享一些共有变量来同步他们的行为。

第一次尝试(单标志法)

共享变量

1
2
int turn = 0;
turn = i; // 表示允许进入临界区的线程ID

线程Ti的代码：

1
2
3
4
5
6
do {
    while(turn != i) ; // 不是i的话进入不了临界区
    critical section
    turn = j;
    remainder section
}while(1);

该方案类似买面包方案四，同样有效。通过修改id交替进入，Ti不在临界区，Tj想要继续运行，但是必须等待Ti进入过临界区以后。满足“忙则等待”，但是有时不满足“空闲则入”

第二次尝试 (双标志法先检查)

先判断，后修改变量

共享变量

1
2
3
int flag[2]; 
flag[0] = flag[1] = 0;
flag[i] == 1//表示线程Ti是否在临界区

线程Ti的代码

1
2
3
4
5
6
7
do {
    while (flag[j] == 1) ;
    flag[i] = 1;
    critical section
    flag[i] = 0;	
    remainder section
} while (1);

对应买面包方案二，二者可能存在同时判断，同时设置，均进入临界区的情况，不满足“忙则等待”

第三次尝试(双标志法后检查)

先修改变量，后判断

共享变量

1
2
3
int flag[2]; 
flag[0] = flag[1] = 0;
flag[i] == 1// 表示线程Ti想要进入临界区

线程Ti的代码

1
2
3
4
5
6
7
do {
    flag[i] = 1;
    while (flag[j] == 1) ;
    critical section
    flag[i] = 0;	
    remainder section
} while (1);

对应买面包的方案三，有可能谁都进入不了临界区，满足“忙则等待”，但是不满足“空闲则入”

Peterson算法(双标志+单标志法)

满足线程Ti和Tj之间互斥的经典的基于软件的解决方法（1981年）

先修改变量，后判断；后修改者等待；只适用于两个进程

共享变量

1
2
int turn;//表示该谁进入临界区
boolean flag[];//表示进程是否准备好进入临界区

进入区代码

1
2
3
flag[i] = true;
turn = j;//写数据总有一前一后，不可能同时完成
while (flag[j] && turn ==j)

退出区代码

1
flag[i] = false;

线程Ti 的代码

1
2
3
4
5
6
7
8
do {
      flag[i] = true;
      turn = j;
      while ( flag[j] && turn == j);
      CRITICAL SECTION
      flag[i] = false;
      REMAINDER SECTION
   } while (true);

j执行时i等待，退出后i可执行

piazza上给出了Peterson算法三个线程的反例

线程0，1，2

1
turn=1，flag[1]=false，flag[0] = true，flag[2] = true

在线程T0和T2的peterson算法实现中，只要flag[j]=true和turn=j任意一个不满足，（理论上）T0，T2就可以进入临界区。由前面假设可得，flag[1] = false，此时while(flag[j]&&turn==j)不足以阻塞T0,T2，两个线程都满足进入临界区的条件，不满足临界区的“忙则等待”规则。

Dekkers算法

线程Ti 的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
flag[0]:= false; flag[1]:= false; turn:= 0;//or1 
	
do {
       flag[i] = true;
       while flag[j] == true { 
            if turn ≠ i { 
               flag[i] := false 
               while turn ≠ i { } 
               flag[i] := true 
            }  
        } 
        CRITICAL SECTION
        turn := j
        flag[i] = false;
        REMAINDER SECTION
   } while (true);

判断复杂，i执行时发现j也想进入，turn此时不为i,则将i自己的标志位改为false，并等待turn修改为i再执行，便于扩展。

进入区：先修改flag，后判断是否有多个想进入；后修改者等待；
退出区：修改turn；
适用于多个进程；

把Dekkers算法中的flag[i] := false去掉后：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
flag[0]:= false; flag[1]:= false; turn:= 0;//or1

do {
     flag[i] = true;
     while flag[j] == true {
       if turn ≠ i {
         while turn ≠ i { }
         flag[i] := true
       } 
     }
     CRITICAL SECTION
     turn := j
     flag[i] = false;
     REMAINDER SECTION
  } while (true);

错误例子：

两个进程都进入do-while循环，而后flag[0] = true且flag[1] = true，同时进入while flag[j] == true循环。这时若果turn=1，则0号进程进入if后在while turn ≠ i 处死循环，1号进程在while flag[j] == true 处死循环。

N线程的软件方法

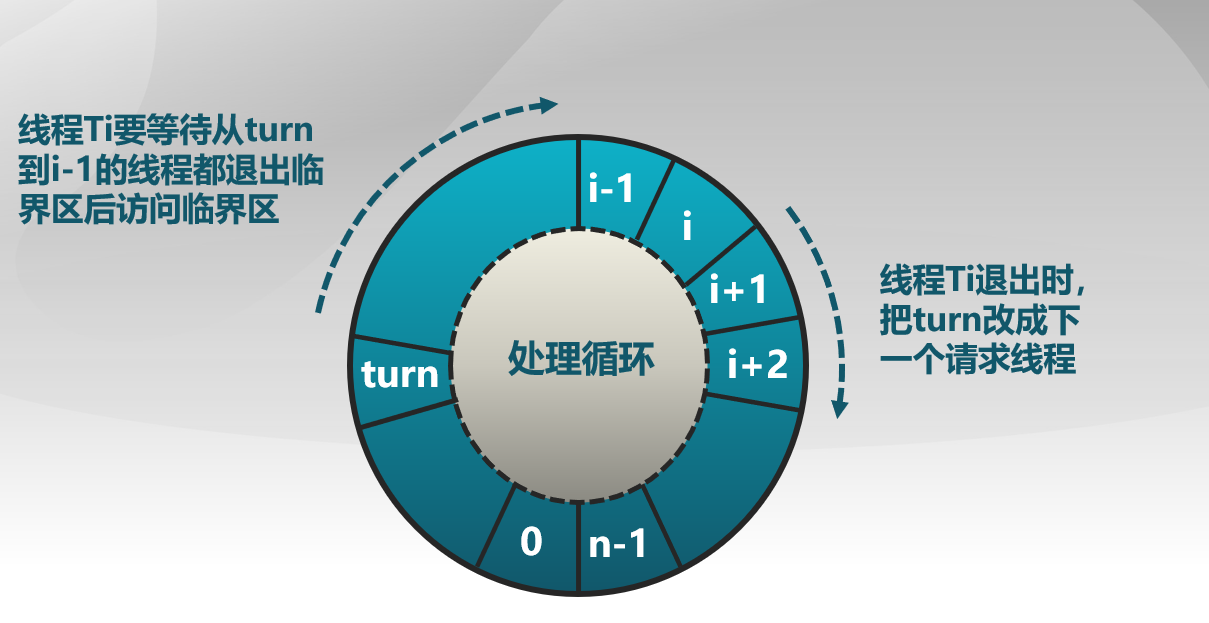
Eisenberg算法

可参考维基百科 ，该算法将n个进程形成一个圈，依照这个圈的顺序来分发资源。

首先这个算法需要维护这样的数据结构：

1
2
3
4
5
shared enum states {IDLE, WAITING, ACTIVE} flags[n];

shared int turn;

int index;        /* not shared! */

其中，flags[i]=IDLE：进程Pi不想进入临界区；

flags[i]=WAITING：进程Pi想进入临界区；

flags[i]=ACTIVE：进程想进或已进临界区。

flags的所有元素初值都是IDLE；

turn的初值为0到n-1之间的任一正整数，它表示允许进入临界区的进程编号；

index为每个进程拥有的一个局部变量，其初值为0到n-1之间的任一正整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
repeat {
    /* announce that we need the resource */
    flags[i] = WAITING; //（0）语句
	//循环1开始
    index = turn;
    while (index != i) {
        if (flag[index] != IDLE) index = turn;//条件1
        else index = index+1 mod n;
    }
    //循环1结尾
    flags[i] = ACTIVE; //（1）语句
	//循环2开始
    /* find the first active process besides ourselves, if any */
    index = 0;
    while ((index < n) && //条件2 
	((index == i) || (flags[index] != ACTIVE)))  //条件3
    {
        index = index+1;
    }
    	//循环2结尾
//最终判断
} until ((index >= n)  //条件4
	&& ((turn == i)|| (flags[turn] == IDLE))); //条件5

我们考虑第i个进程：
turn是一个关键的变量，它决定谁现在能进入临界区。有2种情况：
1.turn是一个随机的值，此时没有任何人申请资源
2.turn是某个申请资源的进程的编号

我们要验证turn到底处于哪一种情况，如果是第一种情况，那么即使turn≠i，我们也可以进入临界区，如果是第二种情况，那么我们得等到turn号进程执行完成。

第零步，初始状态，申请之后，还处于IDLE状态

第一步，进入WAITING状态，并检查[turn,i)区间内有没有申请资源的进程，有则等待它们执行完毕，没有则进入第二步

第二步，进入ACTIVE状态，并试图寻找一个其它的处于ACTIVE状态的进程，如果没找到，则获得资源的控制权，如果找到了，则回到WAITING状态

为何能解决同步互斥问题？
首先有一个序，从turn开始，越前面的进程越优先获得资源。
其次，如果执行到一半，突然有序号在自己之前的进程申请资源，自己会放弃资源的申请，等待序号靠前的进程结束。

正确性证明

互斥进入

实际上循环2就已经实现了互斥进入，即只能有一个进程进入临界区，即只有第一个设置ACTIVE的才有可能进入临界区。 这里的第一个是指在写之前flags全不是ACTIVE，写后第一个变为ACTIVE，如果有进程写了然后循环回去又改成了WAITING，则下一个第一个改ACTIVE的才有可能进入临界区。 因为先设置ACTIVE并还没有循环回去的进程会让其他进程在数ACTIVE数目时都发现不只自己，这样就进不到临界区。因此循环2保证了在临界区没有进程时最多一个进程可能进入临界区。然后，如果有一个进程进入了临界区，那么，该进程的flags必定为ACTIVE，继而阻止了其他所有进程在循环2中将index加到n，所以这时没有进程能再进去，除非临界区的进程退出临界区，改了自己的flags。

综上，互斥进入得证。

空闲则入

下面给出空闲则入的证明：

使用反证法：

如果不满足空闲则入，那么必然存在一种情况，所有进入竞争区的进程都在repeat循环里出不来

首先看repeat循环的特点是，

（a）只要进入了这个竞争区，flags就一定不是IDLE；

（b）最靠近turn的进程必然能够通过循环1

因此，如果所有进程都出不去，那么经过充分而有限的时间t‘（我们假设每个进程都有机会获得CPU），所有竞争区的进程的flags必定都非IDLE，而且在更充分的时间t0后，所有进程在循环1中判断时，涉及的在竞争区内的进程的flags都非IDLE，那么这时，就只有最靠近turn的那个进程能够通过循环1。

即使在这个充分而有限的时间t0内有新进程进入，根据假设，所有进程还是都出不去，那么仍然会有一个时间t1，使只有最靠近turn的那个进程通过循环1，由于进程总数是有限的，所以这种时间的增长是有限的，于是在一个有限的时间t后，只有最靠近turn的那个进程能够通过循环1。

显然，此时这个进程可以通过循环2将index加到n，由于其距离turn最近，说明turn就是该进程或者turn的flags为IDLE，于是该进程进入临界区（即使此时turn对应的那个进程进入repeat改了flags也没关系，只是再次增大了t而已）

综上，假设错误，满足空闲则入.

由此，该算法正确 (只要保证调度过程不会有某一进程在无限时间内获取不到CPU的情况，显然这一点一般是可以保证的)

实际上，只有turn对应的进程没有指向进入repeat的一个进程，并且发生了很多次非常极端的情况时，上面的t才会比较长，而上面证明了t依然有限，所以该算法有效。

基于软件的解决方法分析

  • 复杂 需要两个进程间的共享访问项
  • 需要忙等待 浪费CPU时间，需要频繁查询共享变量

高级抽象的同步方法

硬件提供一些同步原语

  • 中断禁用
  • 原子操作指令(从硬件上保证其原子性)

锁(Lock)

一个抽象的数据结构

  • 一个二进制变量(锁定/解锁)
  • Lock::Acquire()
    • 锁被释放前一直等待，然后得到锁
  • Lock::Release()
    • 释放锁，唤醒任何等待的进程

使用锁来控制临界区访问

1
2
3
lock_next_pid->Acquire();
new_pid = next_pid++;
lock_next_pid->Release();

原子操作指令

现在CPU体系结构提供的特殊原子指令

测试和置位指令(TS Test-and-Set)

  • 从内存单元中读取值
  • 测试该值是否为1(真或假)
  • 内存单元值设置为1
1
2
3
4
5
boolean TestAndSet(boolean *target) {
    boolean rv = *target;
    *target = true;
    return rv:
}

交换指令(Exchange)

交换内存中的两个值

1
2
3
4
5
void Exchange (boolean *a, boolean *b){
    boolean temp = *a;
    *a = *b;
    *b = temp:
}

TS指令实现自旋锁(Spinlock)

1
2
3
4
5
6
7
8
9
10
11
12
class Lock {
    int value = 0;
}
Lock::Acquire() {
   while (test-and-set(value))
      ; //spin
}
//如果锁被释放，那么TS指令读取0并设置为1
//锁将被设置为忙等待状态
Lock::Release() {
    value = 0;
}

如果锁处于忙等待状态，那么TS指令读取1并将值设置为1。

  • 不改变锁的状态且需要循环

TS指令实现无忙等待锁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Lock {
   int value = 0;
   WaitQueue q;
}
Lock::Acquire() {
   while (test-and-set(value)) {
      add this TCB to wait queue q;
      schedule();
      //通过调度让其余进程继续执行
   }
}
Lock::Release() {
   value = 0;
   remove one thread t from q;
   wakeup(t);
}

原子操作指令锁特征

  • 优点
    • 适用于单处理机或者共享内存的多处理机中任意数量的进程同步(禁用中断只适用于单处理机 多处理机的情况下 禁止单个处理机的中断 其他处理机仍然能够响应中断)
    • 简单且容易证明
    • 支持多临界区
  • 缺点
    • 忙等待锁会消耗处理机时间
    • 可能导致饥饿,进程离开临界区时有多个等待进程的情况(并没有按照先来后到的顺序)
  • 死锁
    • 拥有临界区的低优先级进程，但请求访问临界区的高优先级进程获得处理机并等待临界区(低优先级等CPU,高优先级等临界区)

同步方法总结

锁是一种高级的同步抽象方法

  • 互斥可以使用锁来实现
  • 需要硬件支持

常用三种同步实现方法总结

  • 禁用中断(仅限于单处理机)
  • 软件方法(共享变量 条件弱但是复杂)
  • 原子操作指令(单处理机或多处理机均可)