页面置换算法

发表于 2019-06-23 分类于 Systems

虚拟内存只把部分程序放到内存中，虚拟内存单元不一定由实际物理内存单元对应，因此访问的部分可能不在内存中。在内存中无空闲页时，访问的页面必须替换已经存在的某一页面才能放入到内存中。如何选择替换页由页面置换算法实现，其中根据是否区分不同进程的页面，分为局部置换算法和全局置换算法。

概念

功能

当出现缺页异常时需调入新页面且内存已满置换算法选择被置换的物理页面

设计目标

尽可能地减少页面调入调出次数(与程序访问特征有关)
把未来不再访问或短期内不访问的页面调出

页面锁定

描述必须常驻内存的逻辑页面
通常是操作系统的关键代码(必须存在内存中)或要求响应速度的代码和数据(外存中访问太慢)
通过页表中的锁定标志位 (Lock bit)来标记

评价方法

模拟页面置换行为，记录产生缺页的次数
更少的缺页，更好的性能

局部页面置换算法

最优页面置换算法

置换在未来最长时间不访问的页面

算法实现

缺页时，计算内存中每个逻辑页面的下一次访问时间
选择未来最长时间不访问的页面

算法特征

缺页最少，是理想情况
实际系统中无法实现，每次访问序列不同
无法预知每个页面在下次访问前的等待时间
缺页最少，一般作为置换算法的性能评价依据

最优置换算法示例

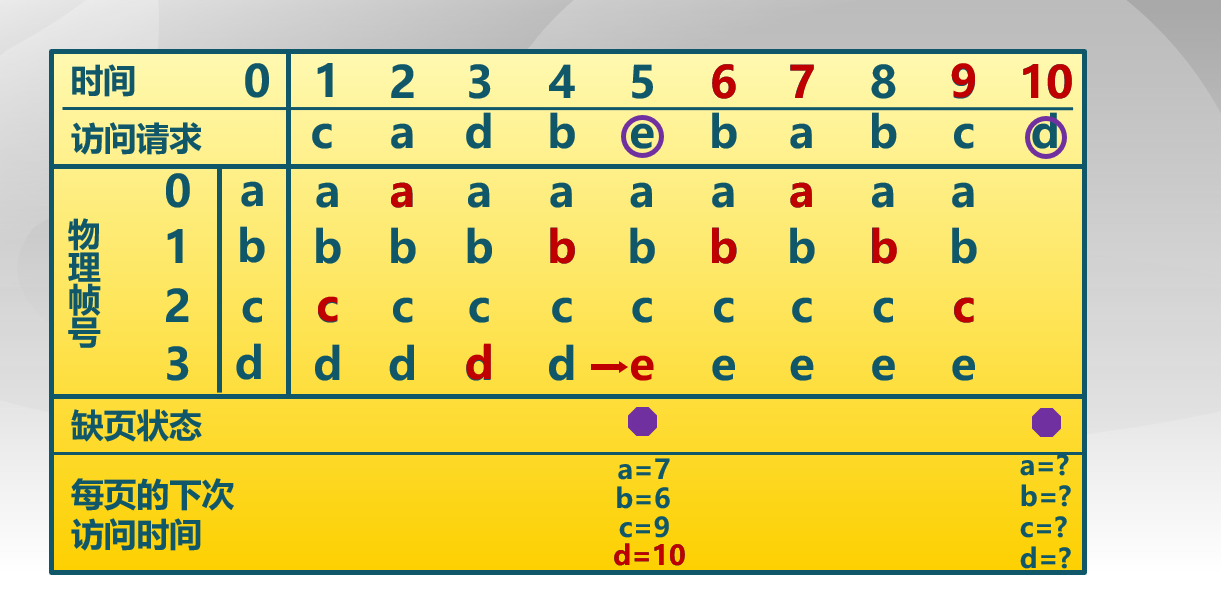
先进先出算法

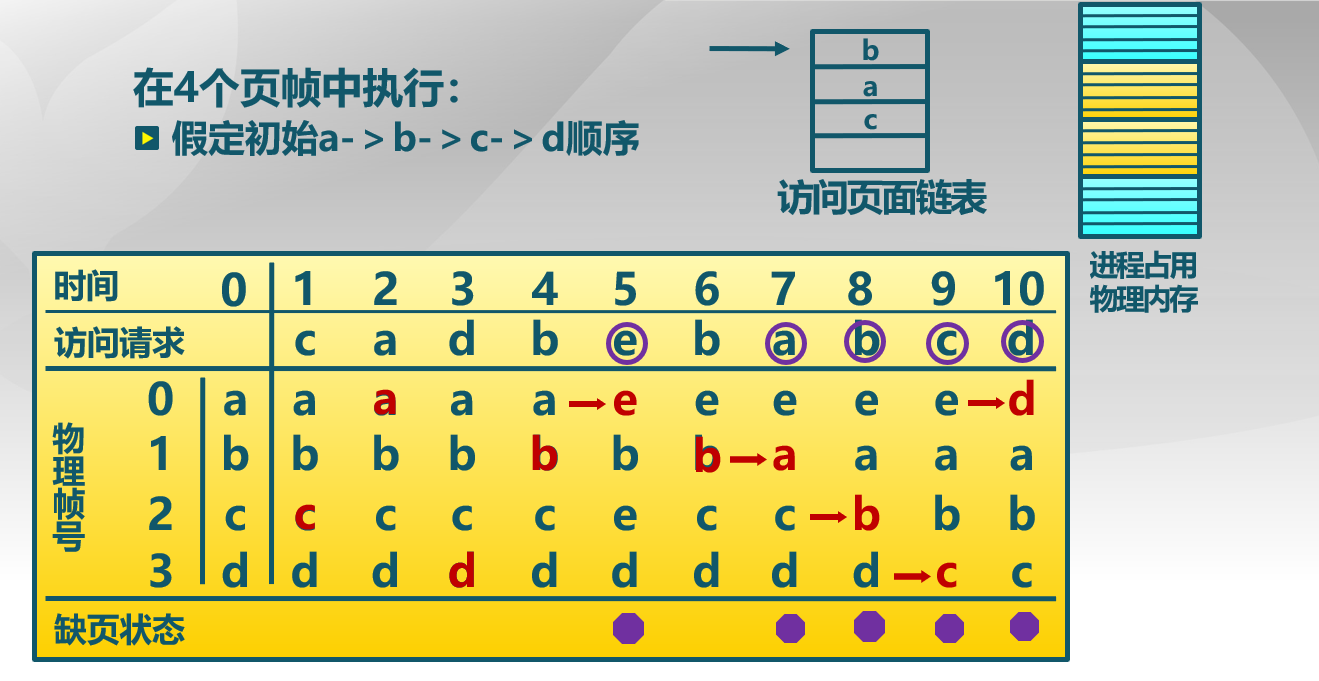
先进先出算法（First-In First-Out, FIFO）

选择在内存驻留时间最长的页面进行置换

具体实现

维护一个记录所有位于内存中的逻辑页面链表
链表元素按驻留内存的时间排序，链首最长，链尾最短
出现缺页时，选择链首页面进行置换，新页面加到链尾

特征

实现简单
性能较差，调出的页面可能是经常访问的
进程分配物理页面数增加时，缺页并不一定减少(Belady现象)
很少单独使用，与其他算法结合

最近最久未使用算法

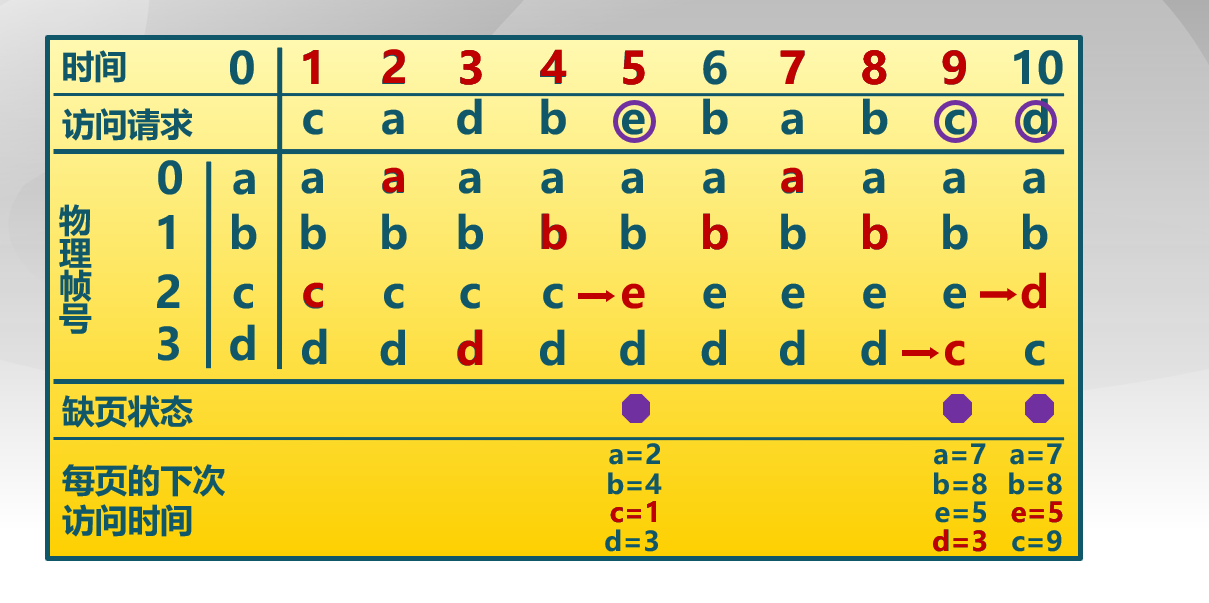
最近最久未使用算法 (Least Recently Used, LRU)

思路考查过去而不是未来

最优置换算法和先进先出算法的折衷
选择最长时间没有被引用的页面进行置换
如某些页面长时间未被访问，则它们在将来还可能会长时间不会访问

实现

缺页时，计算内存中每个逻辑页面的上一次访问时间
选择上一次使用到当前时间最长的页面

LRU算法的可能实现方法

页面链表

系统维护一个按最近一次访问时间排序的页面链表
链表首节点是最近刚刚使用过的页面
链表尾节点是最久未使用的页面
访问内存时，找到相应页面，并把它移到链表之首(落实到每一次访问)
缺页时，置换链表尾节点的页面

活动页面栈

访问页面时，将此页号压入栈顶，并栈内相同的页号抽出(完全搜索一遍，开销太大)
缺页时，置换栈底的页面

特征：开销比较大

时钟置换算法

时钟置换算法（Clock）仅对页面的访问情况进行大致统计，统计过去一段时间内访问特征，若访问过，则留下，若没有访问过，则按照先来后到的顺序进行置换。

数据结构

在页表项中增加访问位，描述页面在过去一段时间的内访问情况
各页面组织成环形链表
指针指向最先调入的页面

算法

访问页面时，在页表项记录页面访问情况
缺页时，从指针处开始顺序查找未被访问的页面进行置换

特征

时钟算法是LRU和FIFO的折中

既不像 LRU 考虑的那么详细，又不像 FIFO只在意一段时间内若不访问就做置换考虑的那么粗

实现

页面装入内存时，访问位初始化为0
访问页面（读/写)时，访问位置1
缺页时，从指针当前位置顺序检查环形链表
- 访问位为0，则置换该页
- 访问位为1，则访问位置0，并指针移动到下一个页面，直到找到可置换的页面

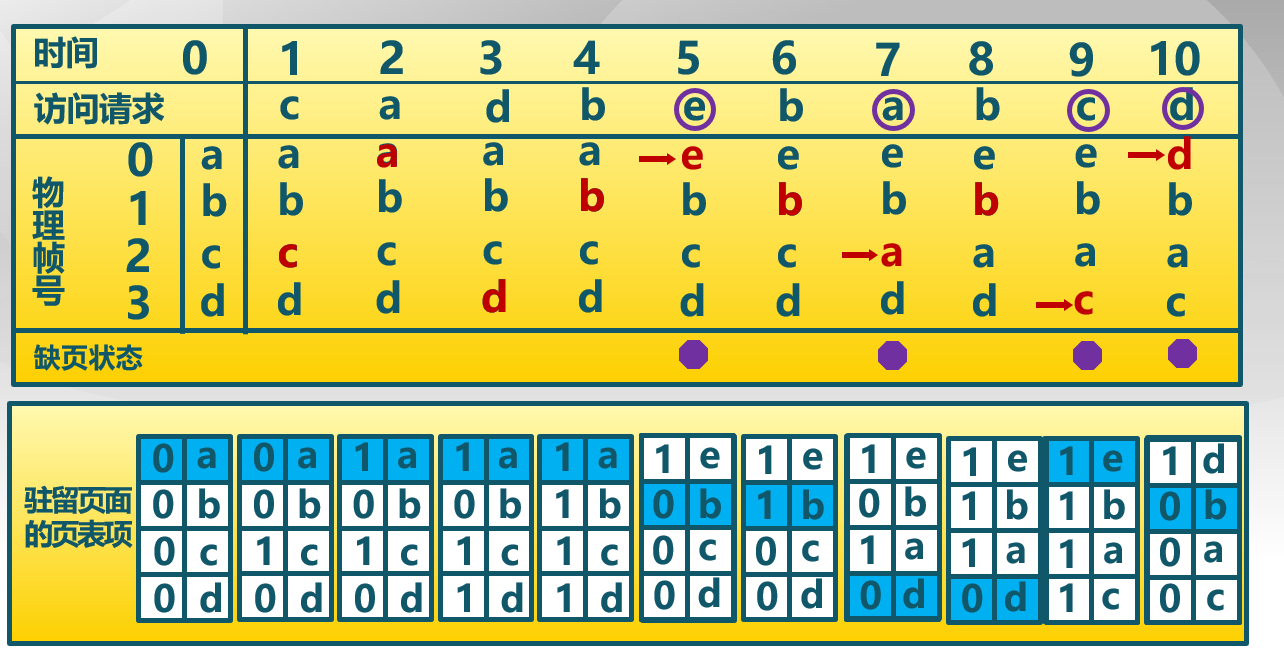
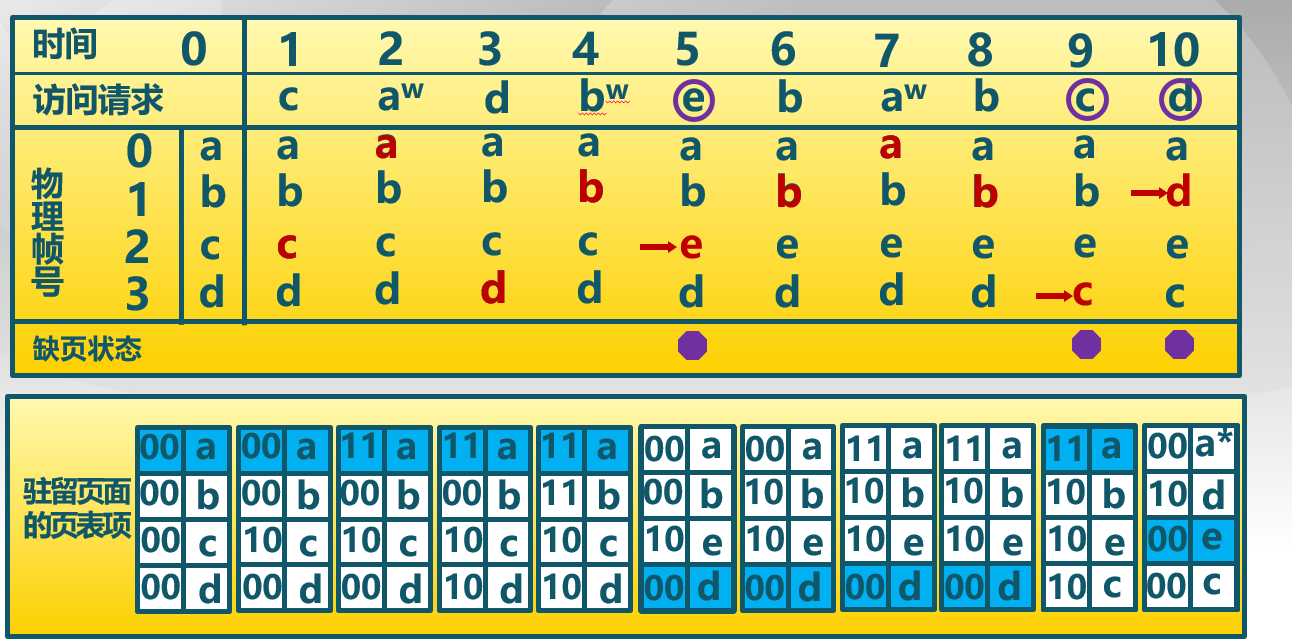
需要特别注意的是：课件中的例子默认为热启动，所以链表的组织顺序为a->b->c->d->a，并不是按照之后的访问顺序来组织链表。每次页面置换后链表指针移至置换页的下一节点，若无页面置换则不移动链表指针。

改进的时钟算法

时钟置换算法中，若置换页被修改过，那么就得先将修改过的页写入到外存，再将需要的页读入内存，处理时间过长，引入改进的时钟算法对写的情况加以考虑从而减少修改页的缺页处理开销。系统定期将修改过的页回到外存中。

算法

在页面中增加修改位，并在访问时进行相应修改
缺页时，修改页面标志位，以跳过有修改的页面

最不常用算法

最不常用算法（Least Frequently Used, LFU）缺页时，置换访问次数最少的页面

实现

每个页面设置一个访问计数

访问页面时，访问计数加1

缺页时，置换计数最小的页面

特征

算法开销大

开始时频繁使用，但以后不使用的页面很难置换

解决方法：计数定期右移

LRU和LFU的区别

LRU关注多久未访问,时间越短越好
LFU关注访问次数，次数越多越好

页面置换算法总结

LRU 和 FIFO本质都是先进先出算法

	排序标准	顺序	belady	开销
LRU	最长时间没有被访问	需要动态地调整顺序	否	大
FIFO	在内存驻留时间最长	页面进入时间是固定不变的	是	小

Clock算法是二者的折衷

页面访问时，不动态调整页面在链表中的顺序，仅做标记
缺页时，再把它移动到链表末尾
对于未被访问的页面，即只访问一次，Clock和LRU算法的表现一样好，均退化为FIFO算法
对于被访问过的页面，Clock算法不能记录准确访问顺序，而LRU算法可以

LRU算法：

排队依据：最近访问时间

访问时操作：将访问到的页面抽出并放到栈顶

缺页时操作：将栈底页面弹出，若该页面未被修改则无需操作，若被修改则将其写回内存。将需要装入内存的页放到栈顶

初始化操作：将初始的栈清空

最优算法：

排队依据：每个逻辑页面下一次访问时间

访问时操作：无

缺页时操作：计算下次访问时间，选择最长时间不访问的页面

初始化操作：依次将各个页面装入栈中

LFU算法：（假设使用优先队列来维护）

排队依据：访问次数。访问次数少的优先级更高。

访问时操作：给该页面的访问次数加1。优先队列需要相应地对该页面的位置做调整。又，如果考虑改进的LFU算法，访问次数的“加1”可能是模意义下的。

缺页时操作：将队首弹出。队首对应的页面计数应该清零。将新页面加入到优先队列中即可。

初始化操作：顺次地，每一个初始页面加入，并设访问次数为1即可。

FIFO算法：（维护一个记录逻辑页面的链表）

排队依据：页面加载时间

访问时操作：无

缺页时操作：将被访问页面对应的索引添加在链表尾。如果需要换出页面，则把链表头对应的页面换出，并把该节点从链表中移除

初始化操作：建立一个空的队列

时钟置换算法

排队依据：按照访问的计数（0/1）

访问时操作：修改访问位为1

缺页时操作：判断指针指向位置访问位是否为0，若为0，则置换该页，若为1，则修改为0，指针指向下一个直到找到一个访问位为0的页面

初始化操作：建立一个页面的环形列表，在页表项中增加访问位，初始化为0；环形链表的指针指向最先调入的页面。

Belady现象

可能出现分配的物理页面数增加，但是缺页次数反而升高的异常现象

原因

算法的置换特征与进程访问内存的动态特征矛盾
置换出去的页面并不一定是进程近期不会访问的页面

下面哪些页面淘汰算法不会产生Belady异常现象

先进先出页面置换算法（FIFO)
时钟页面置换算法（CLOCK)
最佳页面置换算法（OPT）
最近最少使用页面置换算法（LRU）

此处没有提及LFU算法，不恢复计数的LFU算法则可能存在Belady现象，而恢复计数的LFU算法不存在Belady现象。LFU是最近最不常用页面置换算法(Least Frequently Used),也就是淘汰一定时期内被访问次数最少的页。这里需要注意，当某页被换出后，其访问次数会被记录下来为n，当此页被再次访问，并被换入时，此页的访问次数为n+1。在这种定义下的LFU是没有Belady异常的。

当“不恢复上次换出时的访问计数”时LFU出现belady现象的例子：

考虑访存顺序：0 0 1 1 1 2 2 0 0 2 2 3 1 3 1 3 1 3 1 3 1 3 1 …

最后的序列是3号页和1号页的循环。

当物理页帧数为2时，之后的3和1循环段不会出现任何缺页

当物理页帧数为3时，之后的3和1循环段总是缺页

clock算法的belady现象举例

“虚拟页访问序列为 1,2,3,4,1,2,5,1,2,3,4,5，物理页帧数量为3和4”既能导致FIFO的belady现象，也能导致clock算法的belady现象。

LRU算法不存在belady现象的证明

最优置换和LRU算法都没有Belady异常。这两个都属于同一类算法，称为栈算法（stack algorithm），都绝不可能有Belady异常。栈算法可以证明为：对于帧数为n的内存页集合是对于帧数为n+1的内存页集合的子集。对于LRU算法，如果内存页的集合为最近引用的页，那么对于帧的增加，这n页仍然是最近引用的页，所以也仍然在内存中。

证明：
        原理:因为小的物理页帧的栈包含于大数目的物理页帧的栈
        下证s(t) 始终包含于 s'(t)
            利用归纳法，假设 1<=i<=t-1 时 s(i)包含于s'(i)，现在要证s(t)依然包含于s'(t)
            (1) b(t)同时属于s(t)和s'(t)：此时s(t)和s'(t)都不发生变化，满足包含关系；
            (2) b(t)不属于s(t),属于s'(t)：s(t) 替换后，由于b(t)∈s(t)，所以s(t)包含于s'(t)
            (3) (1)和(2)很容易证明，
                对于b(t)同时不属于s(t-1)和s'(t-1)的情况，我们依然按照视频里栈的方式对s(t-1)和s'(t-1)排序
                由于s(t-1)包含于s'(t-1),所以s(t-1)内每一个元素都存在于s'(t-1)中。
                现在两个栈都是按最后一次访问的时间的顺序来排列的，由于s(t)在进行替换时会替换s(t-1)里面最长时间没被访问的元素(栈底)，设为a,那么a显然也存在于s'(t-1)里面，并且它不一定是s'(t-1)的栈底。
                    A. 当a是s'(t-1)的栈底时，s(t)和s'(t)替换的都是a, s(t) = s(t-1) - {a} + {b(t)} , s'(t) = s'(t-1) - {a} + {b(t)}
                    B. 当a不是s'(t-1)的栈底时，则s'(t-1)的栈底c必然不属于s(t-1)，否则就会与a是s(t-1)的栈底矛盾（即c比a有更长的时间未被访问），此种情况下s(t)和s'(t)依然满足包含关系
            (4) 由归纳假设可以得知此种情况不存在

恢复计数的LFU算法不会出现Belady现象的证明

首先对恢复计数的LFU算法进行一种感性认识：考虑这样一个大小为n的栈S，它能够实时维护当前内存中存在的所有页面，并总能保持从栈顶到栈底存放的页面的访问次数是递减的。那么，需要置换的时候，被换出去的总是当前存在栈底的页面。又，在恢复计数的条件下，各个页面按计数多少排出的顺序总是一致的，且与系统分配的页面个数没有关系。事实上，考虑分配了无穷多个页面的情况：这时，相应的栈S∞总不会有页面被置换出来，那么总有S⊂S∞（这种包含关系是序列的包含）。我们认识到，页面的计数与栈的容量无关。
下面来进行证明。设t时刻下大小为n的栈的内容为有序集S(t)，大小为n+k的栈的内容为有序集S′(t)，其中k>0；又，B(t)为新入栈的元素。

只需证明，对于任意t，S(t)⊂S′(t)，且任意S(t)中元素a，对应到S′(t)中元素a′，满足a的位置小于等于a′的栈位置，即可证明物理页面数量增加的缺页率不会降低。
使用数学归纳法。

基础：在初始情况下，S(0)与S′(0)都为空，满足任意S(0)中元素a，对应到S′(0)中元素a′。

归纳：假设在t−1时刻满足S(t−1)⊂S′(t−1)，且任意S(t−1)中元素a，对应到S′(t−1)中元素a′，满足a的位置小于等于a′的栈位置。则在t时刻，对于B(t)页的页面访问请求，可能出现以下三种情况：
1. B(t)∈S(t) 且 B(t)∈S′(t)。记B(t)在S(t)中的位置是b，在S′(t)中的位置是b′，则b≤b′。经过访问后，要给两个占中的该页面计数各加一。若B(t)在S(t)中上移超过了Δb个页面，则由于这Δb个页面均有序地存在于S′(t−1)中，故B(t)在S′(t)中至少也上移了Δb。这样，b+Δb≤b′+Δb，性质仍保持；
2. B(t)∉S(t) 且 B(t)∈S′(t)。这时将B(t)页面重新加入到S中。假设B(t)最终落在S(t)的位置b上，也就是说B(t)的计数超过了S(t−1)中的低b个；由于S(t−1)⊂S′(t−1)，那么S(t−1)中的低b个也依次存在于S′(t−1)中。由于页面的计数与栈的容量无关，我们知道S′中B(t)下面至少有这低b个页面，故其落在的位置一定大于等于b。
3. B(t)∉S(t) 且 B(t)∉S′(t)。这时将B(t)页面重新加入到S和S′中。假设B(t)最终落在S(t)的位置b上，也就是说B(t)的计数超过了S(t−1)中的低b个；由于页面的计数与栈的容量无关，且S(t−1)中的低b个页面也属于S′(t−1)中，对应在S′中的位置至少是低b个。那么，B(t)的计数也一定超过了S′(t−1)中的低b个，最终落在落在S′(t)的位置一定大于等于b。
由于假设的存在，S(t)⊂S′(t)，即不会出现B(t)∈S(t) 且 B(t)∉S′(t)的情况。
综上所述，由数学归纳法得，对任意时刻t，S(t)⊂S′(t)，且任意S(t)中元素a，对应到S′(t)中元素a′，满足a的位置小于等于a′的栈位置。
即对任意时刻，对S′(t)的缺页数量不会大于S(t)；物理页数量增加，缺页率不会上升。
因此，恢复计数的LFU算法不会出现Belady现象。

OPT算法不会出现Belady现象的证明

设帧数为n时，内存中逻辑页面的集合为S(n)，可以证明在任意时间 S(n)⊆S(n+1)
设L(n)表示将S(n)中元素按将来访问时间排序从大到小排序的结果。
在访问序列中，按第一次出现的顺序，将逻辑页面编号为1, 2, 3, ...（如访问顺序为1, 2, 1, 3, 2, 4...)，并令tk表示编号为k的页面第一次出现的时间
假设：每一个时间点 t，都有 S(n)⊆S(n+1)。
证明如下：
t = 0 时，S(n) = S(n+1) = ∅，满足假设
t<tn+1时，此时S(n)和S(n+1)的物理帧还没满，所以发生缺页时都会填入新页
tk−1<t<tk,k≤n+1，访问的页面编号不超过k - 1，而这些页面在之前已经被加载，所以不发生页缺失，S(n) = S(n+1) = {1, 2, ..., k-1}，满足假设
t=tk,k≤n，第一次访问编号k的页面，同时发生缺失，之后S(n)  = S(n+1) = {1, 2, ..., k}, 满足假设
t=tn+1时
此时，S(n)和S(n+1)同时发生缺页，S(n)换出一页再换入编号为n+1的页，而S(n+1)直接加载编号为n+1的页，所以S(n)⊆S(n+1)。
t>tn+1时，S(n)和S(n+1)的物理内存都已经满了，可用归纳法证明上述假设
初始状态 t=tn+1时，满足假设（见3）
假设t = m 时有S(n)⊆S(n+1)，则当t = m + 1时
如果S(n)和S(n+1)都访问正常，则S(n)和S(n+1)都不发生变化。
如果S(n)访问异常，S(n+1)访问正常，设访问前S(n+1)=S(n)∪{x}，那么易知此时访问的是x，所以S(n)换出一页再换入x后，仍然满足S(n)⊆S(n+1)
如果S(n)和S(n+1)均访问异常，设访问前S(n)={s1,s2,...,sn}, S(n+1)={s1,s2,...,sn,x}，将两者中元素按未来访问时间从大到小排序，可得到L(n)为{s′1,s′2,...,s′n−1,s′n}, L(n+1)为{s′1,s′2,...,s′i,x,s′i+1,...,s′n}
如果x<s′n，则S(n)换出s'n, S(n+1)换出x, 再同时换入新页，依然满足S(n)⊆S(n+1)
如果x>s′n, 则S(n)和S(n+1)同时换出s′n换入新页，所以满足S(n)⊆S(n+1)
综上所述，可以证得。

所以易证不会出现Belady现象

全局置换算法

局部页面置换算法没有考虑到进程访存的差异，在不同阶段进程需求不同。局部页面置换算法分配页面数始终一致无法适应需求，在某些情况下增加页面会大大减小缺页次数。因此，引入全局置换算法，为进程分配可变数目的物理页面。

全局页面置换算法需要解决的问题

进程在不同阶段的内存需求是变化的
分配给进程的内存也需要在不同阶段有所变化
全局置换算法需要确定分配给进程的物理页面数

工作集算法

CPU利用率与并发进程数的关系

进程数少时，CPU利用率与并发进程数会相互促进；

进程数较多导致局部性降低时，CPU利用率与并发进程数会相互制约；

工作集

工作集：当前进程正在使用的逻辑页面的集合；即当前一段时间t内进程访问的所有逻辑页面的集合。

工作集的变化规律：

进程开始执行时 随着访问新页面逐步建立较稳定的工作集。

工作集稳定期 当内存访问的局部性区域的位置大致稳定时，工作集大小也大致稳定

工作集过渡期 局部性区域的位置改变时，工作集快速扩张和收缩过渡到下一个稳定值

常驻集

当前时刻进程实际驻留内存的页面集合

工作集和常驻集的关系
- 工作集是进程运行过程中固有的性质 (进程在一段时间访问的页面集合)
- 常驻集取决于系统分配给进程的物理页面数和页面置换算法
缺页率和常驻集的关系
- 常驻集包含工作集时缺页较少 (进程访问的页都在内存中)
- 工作集发生剧烈过渡时，缺页较多
- 进程常驻集大小达到一定数目后，缺页率不会明显下降

工作集置换算法

换出不在工作集中的页面(并不一定在缺页时执行)

窗口大小τ：当前时刻前τ个内存访问的页引用是工作集，τ被称为窗口大小
实现方法：
- 访存链表：维护窗口内的访存页面链表
- 访存时，换出不在工作集的页面；更新访存链表
- 缺页时，换入页面；更新访存链表

缺页率算法

缺页率(page fault rate)

缺页次数 / 内存访问次数或缺页平均时间间隔的倒数

缺页率置换算法（PFF, Page-Fault-Frequency）

通过调节常驻集大小，使每个进程的缺页率保持在一个合理的范围内
若进程缺页率过高，则增加常驻集以分配更多的物理页面
若进程缺页率过低，则减少常驻集以减少它的物理页面数

实现

缺页时计算从上次缺页时间$t_{last}$ 到现在$t_{current}$ 的时间间隔
- 如果$t_{current} - t_{last} > T$ 缺页率低于设定值,则置换所有在$[t_last, t_current]$中没有被引用的页
- 如果$t_{current} - t_{last} <= T$ 缺页率高于设定值,则增加缺失页到常驻集中

抖动问题

由于分配给进程的物理页面太少无法包含工作集导致大量缺页而频繁置换，从而进程运行速度变慢。

原因

随着驻留内存的进程数目增加，分配给每个进程的物理页面数不断减小，缺页率不断上升。

通过调节并发进程数来进行系统负载控制。

最佳状态是：平均缺页间隔 = 缺页异常处理时间。