算法导论

发表于 2019-08-28 分类于 Algorithm

算法一词在古籍中最早见于周髀算经，对应的algorithm一词来自于波斯数学家al-Khwarizmi ，均以数学语言描述。最早的算法在线性方程组中用到，其中的欧几里得算法为史上第一个算法。算法一词在日常生活中也越来越普遍，究竟什么才可以称为算法呢？我们又可以怎样衡量算法效率呢？

算法

算法是计算机程序的数学抽象，基于特定的计算模型，旨在解决某一信息处理问题而设计的指令序列。

算法具有以下特性：

输入待处理的信息(问题)
输出 经处理的信息(答案)
正确性 的确可以解决指定的问题
确定性 任一算法均可以描述为一个由基本操作组成的序列
可行性 每一基本操作都可实现，且在常数时间内完成
有穷性 对于任何输入，经有穷次操作，都可以得到输出

计算的过程即为信息处理的过程，输入信息经算法处理后得到输出信息。计算模型为计算机的抽象，各层次间抽象对应关系为：

程序	算法
编程语言	伪代码
计算机	计算模型

其中，算法建立在伪代码之上，伪代码建立于计算模型之上，类似的，程序基于编程语言，编程语言基于计算机实现。

计算模型

在实际环境中直接测得的执行时间，可作为衡量算法效率的指标。可是即便是同一输入，同一算法，在不同的硬件平台上、不同的操作系统，所需要的时间都不尽相同。在图灵机、随机存储机等计算模型中，指令语句均可分解为若干次基本操作，比如算术运算、比较、分支、子程序调用和返回等，在大多数实际计算环境中，每一次这类基本操作都可在常数时间内完成。这样一来，可以将时间复杂度理解为算法中各条指令的执行时间之和，从而统一衡量各个算法的效率。

计算模型指定了：

算法的基本操作
每种操作的成本(时间，空间)

RAM

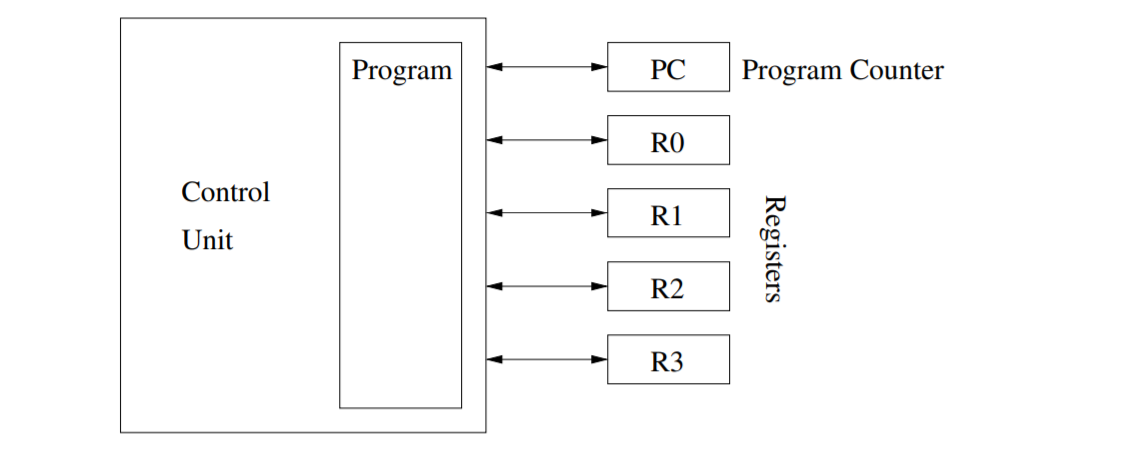
TIM截图20190828113648.png

RAM(random access machine)由只读的输入纸带，只写的输出纸带和内存组成。内存由一系列无限宽度的寄存器组成，寄存器按照顺序编号，总数无限制。控制单元存储程序，即一系列语句，由程序计数器来指定下一个执行的语句。

在常数时间内，可以执行以下操作：

将值读入到寄存器中
寄存器进行简单的加减乘除运算
将寄存器的值存储到内存中
通过寄存器号访问对应的寄存器

在哪些方面，现代电子计算机仍未达到RAM模型的需求

现代电子计算机的寄存器数量有限，无法为无限总数，字长有限，无法存储任意宽度的整数。

图灵机

图灵的基本思想是用机器来模拟人们用纸笔进行数学运算的过程，他把这样的过程看作下列两种简单的动作：

在纸上写上或擦除某个符号；
把注意力从纸的一个位置移动到另一个位置；

而在每个阶段，人要决定下一步的动作，依赖于

（a）此人当前所关注的纸上某个位置的符号

（b）此人当前思维的状态。

为了模拟人的这种运算过程，图灵构造出一台假想的机器，该机器由以下几个部分组成：

一条无限长的纸带TAPE。纸带被划分为一个接一个的小格子，每个格子上包含一个来自有限字母表的符号，字母表中有一个特殊的符号表示空白。纸带上的格子从左到右依次被编号为0, 1, 2, …，纸带的右端可以无限伸展。
一个读写头HEAD。该读写头可以在纸带上左右移动，它能读出当前所指的格子上的符号，并能改变当前格子上的符号。
一套控制规则TABLE。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作，并改变状态寄存器的值，令机器进入一个新的状态，按照以下顺序告知图灵机命令：

写入（替换）或擦除当前符号；

移动 HEAD， ‘L’向左， ‘R’向右或者’N’不移动；

保持当前状态或者转到另一状态
一个状态寄存器。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的，并且有一个特殊的状态h，称为停机状态。

借助计算模型简化和抽象一般计算工具，使我们可以独立于具体的平台对算法的效率给出可信的评价与评判。

T(n)=算法为求解规模为n的问题所需执行的基本操作次数。

在计算模型中，算法的运行时间正比于算法需要执行的基本操作次数。

渐进分析

渐进分析符号，也即我们常说的大O记号，以$O、\Theta、 \Omega$ 这三种符号表示。

$f(x)=\Theta(x^2)$ 的形式与函数类似，却不是函数。$f(x)=\Theta(x^2)$意味着$f(x)$的一个上界和一个下界。如图所示，$f(x)$介于$0.9x^2$的下界和$1.2x^2$的上界之间，二者与$O$内的函数仅仅只差了一个常数项。

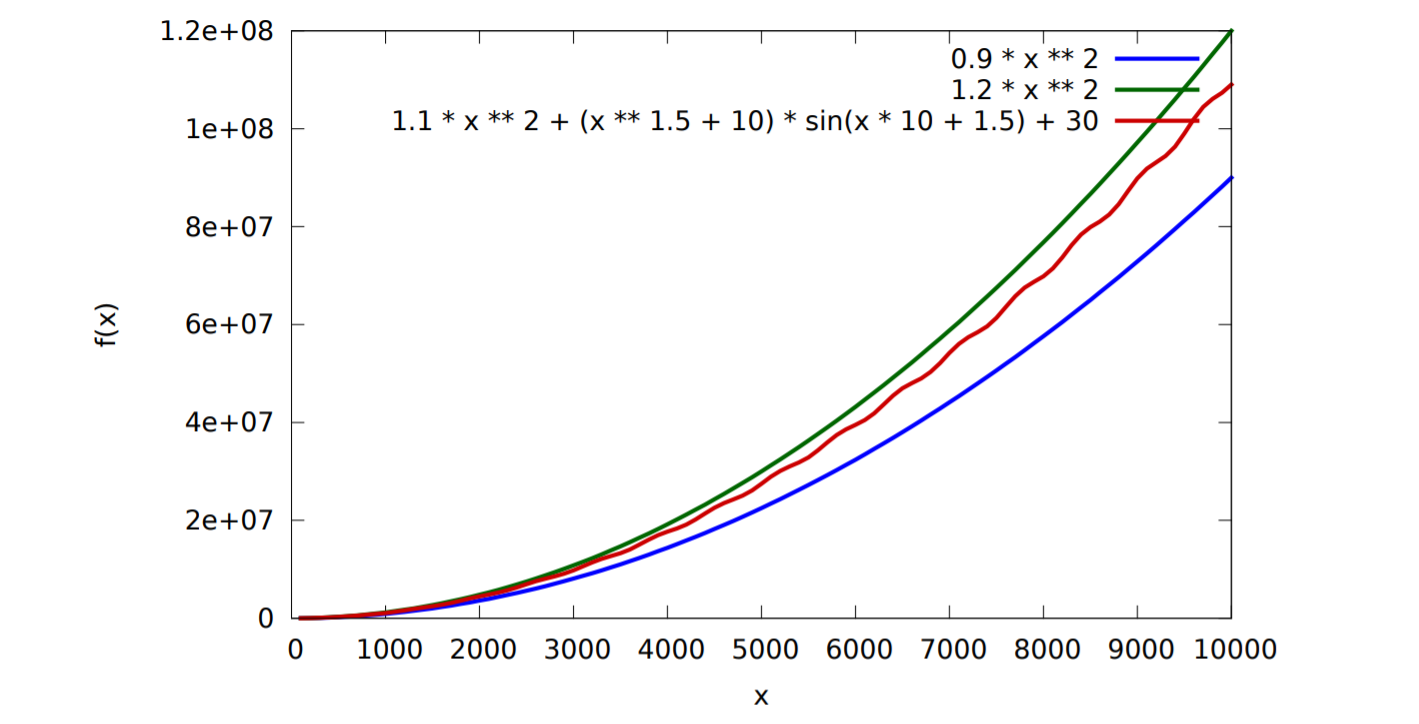
$\Theta$从上界和下界同时限制了函数，$O$从上界限制了函数,$\Omega$从下界限制了函数。

常数

$2019^ {2019}=O(1)$

渐进而言，再大的常数，也小于递增的变数。

这类算法的效率最高，通常不含循环、分支、子程序等，但是具体分析视执行次数而定。

对数

常底数无所谓，$log_an=log_ablog_bn=\Theta(log_bn)$

常数次幂无所谓，$log n^c=clogn=\Theta(logn)$

这类算法非常有效，算法复杂度无限接近于常数，

任意$c>0$,$logn=O(n^c)$

多项式

取多项式指数最高的一项，即

$a_kn^k+a_{k-1}n^{k-1}+…+a_1n+a_0=O(n^k)$

线性：所有$O(n)$类函数

指数复杂度

指数：$T(n)=a^n$

此类算法的计算成本增长极快，通常被认为不可忍受，从$n_c$到$2^n$ 是从有效算法到无效算法的分水岭。

随着问题输入规模的增大，同一算法所需的求解时间通常都呈现单调增加的趋势，但可能随着输入规模的增大，同一算法所需的计算时间可能上下波动。

算法分析

算法分析有两个主要任务，

正确性的证明，即不变性和单调性的证明
复杂度分析，时间复杂度和空间复杂度的分析

c++等高级语言的基本指令，均等效于常数条RAM的基本指令，在渐进分析下二者大体相当，所以可通过分析基本指令的执行次数来分析算法效率。

复杂度分析

随着输入规模的扩大，算法的执行时间的变化趋势可表现为输入规模的一个函数，称作该算法的时间复杂度。

具体地，特定算法处理规模为$n$的问题所需的时间可记作$T(n)$

复杂度分析主要方法：

迭代：将所有基本操作的执行次数累加，即级数求和
递归：递归跟踪，分析递归实例情况，推导递推方程

算数级数：与末项平方同阶

幂方级数：比幂次高出一阶

$T(n)=1^2+2^2+…+n^2=O(n^3)$

$T(n)=1^3+2^3+…+n^3=O(n^4)$

几何级数：与末项同阶

$T(n)=a^0+a^1+a^2+a^3+…+a^n=O(a^n)$

收敛级数：

$\sum_{k=1}^{n} \frac{1}{k^2} <1+\frac{1}{2^2}+…=O(1)$

可能未必收敛，但是长度有限：

1)调和级数：$h(n)=1+1/2+1/3+1/4+1/5+…+1/n=\Theta(logn)$

2)对数级数：$log1+log2+log3+log4+…+logn=log(n!)=\Theta(nlogn)$

正确性

给定n个整数，将它们按照非降序排列

起泡排序

依次比较每一对相邻元素，若逆序则交换之。若整趟都没有进行交换，则排序完成，否则再进行一趟扫描交换。

不变性：经$k$趟扫描交换后，最大的$k$个元素必然就位

单调性：经$k$趟扫描交换后，问题规模缩减至$n-k$

正确性：经至多$n$趟扫描后，算法必然终止，且能给出正确解答。

其中，单调性通常指问题的有效规模会随着算法的推进不断递减。不变性则不仅应在算法初始状态下自然满足，而且应与最终的正确性相呼应。

性能

最坏情况：输入数据反序排列，共$n-1$趟扫描交换

第$k$趟中，需做$n-k$次比较和$3(n-k)$次移动

累计

移动次数$=3n(n-1)/2$

比较次数$=(n-1)+(n-2)+…+1=n(n-1)/2$

$T(n)=4n(n-1)/2$

最好情况：所有输入元素已经完全有序

外循环仅一次，做$n-1$次比较和$0$次元素交换

迭代与递归

计算任意n个整数之和

线性递归 逐一取出并累加各个元素

int sumI ( int A[], int n ) { //数组求和算法（迭代版）
   int sum = 0; //初始化累计器，O(1)
   for ( int i = 0; i < n; i++ ) //对全部共O(n)个元素，逐一
      sum += A[i]; //累计，O(1)
   return sum; //返回累计值，O(1)
} //O(1) + O(n)*O(1) + O(1) = O(n+2) = O(n)

减而治之

为了求解一个大规模的问题，

将其划分为两个子问题，其一平凡，另一规模缩减，
分别求解子问题，
由子问题的解得到原问题的解答。

递归跟踪分析：

整个算法所需的计算时间应该等于所有递归实例的创建、执行和销毁所需的时间总和。检查每个递归实例，累计所需时间(调用语句本身计入对应的子实例)，其总和即为算法执行时间。在空间上，递归调用的空间复杂度正比于最大递归深度。

线性递归

int sum ( int A[], int n ) { //数组求和算法（线性递归版）
   if ( 1 > n ) //平凡情况，递归基
      return 0; //直接（非递归式）计算
   else //一般情况
      return sum ( A, n - 1 ) + A[n - 1]; //递归：前n - 1项之和，再累计第n - 1项
}

递归跟踪分析

每个递归实例只需要常数时间，递归深度为$n+1$

$T(n) = O(1)*(n + 1) = O(n)$

递推方程分析

从递推的角度来看，为求解sum(A,n) ,需递归求解规模为$n-1$的问题sum(A,n-1) ,再累加上A[n-1].

递推方程

$T(n)=T(n-1)+O(1)$

$T(0)=O(1)$

$T(n)=O(n)$

分而治之

二分递归

int sum ( int A[], int lo, int hi ) { //数组求和算法（二分递归版，入口为sum(A, 0, n - 1)）
   if ( lo == hi ) //如遇递归基（区间长度已降至1），则
      return A[lo]; //直接返回该元素
   else { //否则（一般情况下lo < hi），则
      int mi = ( lo + hi ) >> 1; //以居中单元为界，将原区间一分为二
      return sum ( A, lo, mi ) + sum ( A, mi + 1, hi ); //递归对各子数组求和，然后合计
   }
} //O(hi - lo + 1)，线性正比于区间的长度

递归跟踪分析

$T(n)$为各层递归实例所需时间之和，

$T(n)=O(1)(1+2+…+n)=o(1)(2n-1)=O(n)$

递推方程分析

$T(n)=2T(n/2)+O(1)$

$T(0)=O(1)$

$T(n)= O(n)$

从数组区间A[lo,hi)找出最大的两个整数A[x1],A[x2],比较的次数尽可能少

迭代版本1

无论如何，比较次数总是$2n-3$次

void max2(int a[],int lo,int hi,int& x1,int& x2){
    for(x1=lo;int i=lo+1;i<hi;i++){
	    if(a[x1]<a[i]) x1=i;
	}
	for(x2=lo,int i=lo+1;i<x1;i++){
	    if(a[x2]<a[i]) x2=i;
	}
	for(int i=x1+1;i<hi;i++){
	     if(a[x2]<a[i] x2=i;
    }
}

迭代版本2

void max2(int a[],int lo,int hi,int& x1,int& x2){
     if(a[x1=lo]<a[x2=lo+1]) swap(x1,x2);
	 for(int i=lo+2;i<hi;i++){
	     if(a[x2]<a[i]){
		   if(a[x1]<a[x2=i]){
		      swap(x1,x2);
		    }
		}
	}
}

最好情况：$1+(n-2)=n-1$

最坏情况：$1+(n-2)2=2n-3$

迭代版本3

void max2(int a[],int lo,int hi,int& x1,int& x2){
     if(hi<=lo+3) {trivial(A,lo,hi,x1,x2);return;}
     int mi=(lo+hi)/2;
     int x1L,x2L;
     max2(A,lo,mi,x1L,X2L);
     int x1R,x2R;
     max2(A,mi,hi,x1R,x2R);
     if(A[x1L]>A[x1R]){
         x1=x1L;x2=A[x2L]>A[x1R]?x2L:x1R;
     }
     else{
         x1=x1R;X2=A[x1L]>A[x2R]?X1L;x2R;
     }
}//1+1=2;

时间复杂度分析如下：

$T(n)=2T(n/2)+2\leq 5n/3-2$

$G(n)=T(n)+2$

$G(n)=2T(n/2)$

$G(n)=2T(n/2)=4G(n/4)=8G(n/8)$

如果不考虑取整问题，

$G(n)=(n/3)G(n/(n/3))=(n/3)G(3)$

$G(n)=(n/2)G(2)$

$G(2)$和$G(3)$为递归基，

$T(3)\leq 3$

$G(3)=T(3)+2\leq5$

$G(n)\leq(5/3)n$

$T(2)=1$

$G(2)=T(2)+1=3$

$G(n)=(3/2)n$

取较大者，$G(n)\leq(n/3)G(3)\leq(5/3)n$

$T(N)=G(n)-2\leq(5/3)n-2$

以上为粗略的放缩

$T(n)=\lceil{3n/2} \rceil -2$

证明如下：

算法的具体过程为：

将原问题划分为两个子问题，分别对应于向量的前半部分和后半部分
递归求解两问题的解，只需两次比较操作即可得到原问题的解

若前一子向量中最大、次大元素分别为$a_1$,$a_2$,后一子向量分别为$b_1$,$b_2$,则全局最大元素必然取自$a_1$，$b_1$之间，不失一般性地，设：

$a_1=max(a_1,b_1)$

于是全局的次大元素必然取自$a_2$，$b_1$

$max(a_2,b_1)$

由以上分析可得边界条件和递推方程如下：

$T(n)=2T(n/2)+2$

$T(2)=1$

若令$S(n)=(T(n)+2)/2$

则有

$S(n)=S(n/2)=…=S(2)=3/2$

故有$T(n)=\lceil{3n/2} \rceil -2$

这里的关键性技巧在于，合并子问题的解可以仅需要两次而不是三次操作，否则，递归关系应该是：

$T(n)=2T(n/2)+3$

$T(n)=2n-3$

抽象数据类型

各种数据结构可看作是若干数据项构成的集合，同时对数据项预定义一组标准的操作。将数据项和对应的操作视为一个整体，从而将数据结构的外部实现和其内部实现相分离。数据集合和对应的操作可超脱于具体的程序设计语言和具体的实现方式。

抽象数据类型由数据模型和定义在该模型上的一组操作，为外部的逻辑特性，不涉及数据的存储方式。

数据结构为内部的表示与实现，实现抽象数据类型的一系列存储和读取信息的算法。其中存储信息的操作称为更新，读取信息的操作称为查询。

例如，有序列表支持以下操作：

查询：min(),max(),search(x)
更新：insert(x),delete(x)

数据结构的特性为表示不变量(representation invariant)，指明了信息如何存储。不变量是一种属性，在程序运行时总是一种状态。表示不变量确保数据结构正常运行。只要表示不变性仍然保持，那么查询就会得到正确的结果。更新操作需确保更新后表示不变量仍然满足。

例如，有序向量的表示不变量为存储在向量中的关键值必然有序。二分查找在向量有序时必然是正确的，另一方面，插入时需保持向量的表示不变量。

局限

缓存

就地(仅用常数辅助空间)将数组A[0,N)中的元素向左循环移动k个单元

蛮力版

int shift0 ( int* A, int n, int k ) { //蛮力地将数组循环左移k位，O(nk)
   if ( k < 1 ) return 0; int mov = 0;
   while ( k-- ) { //反复以1为间隔循环左移，共迭代k次
      mov += shift ( A, n, 0, 1 );                                 
   }
   return mov;
}

迭代版

int shift1 ( int* A, int n, int k ) { 
   if ( k < 1 ) return 0;
   int mov = 0, s = 0;
   while ( mov < n ) { //O(GCD(n, k)) = O(n*k/LCM(n, k))
      mov += shift ( A, n, s++, k );                                 
   }
   return mov;
}

其中shift实现如下：

int shift ( int* A, int n, int s, int k ) { //从A[s]出发，以k为间隔循环左移，O(n / GCD(n, k))
   int bak = A[s]; //备份起始元素
   int i = s, j = ( s + k ) % n; //从该元素出发
   int mov = 0; //移动次数
   while ( s != j ) { //以k为间隔
      A[i] = A[j]; //依次左移k位
      i = j; j = ( j + k ) % n; mov++;
   }
   A[i] = bak; //将起始元素转入对应位置
   return mov + 1;
}

通过GCD(n, k)轮迭代，将数组循环左移$k$位，时间复杂度为O(n)。$[0,n)$由关于$k$的gcd(n,k)个同余类组成，shift(s,k)只能够使其中一个同余类就位。

倒置版

int shift2 ( int* A, int n, int k ) { //借助倒置算法，将数组循环左移k位，O(3n)
   k %= n; //确保k <= n
   reverse ( A, k ); //将区间A[0, k)倒置：O(3k/2)次操作
   reverse ( A + k, n - k ); //将区间A[k, n)倒置：O(3(n - k)/2)次操作
   reverse ( A, n ); //倒置整个数组A[0, n)：O(3n/2)次操作
   return 3 * n; //返回累计操作次数，以便与其它算法比较：3/2 * (k + (n - k) + n) = 3n
}

该算法需要更多的元素交换操作，但是实际计算效率远远优于其余版本。究其原因在于，reverse涉及的数据元素在物理上是连续分布的，操作系统的缓存机制可以轻易地被激活，并充分发挥作用。其余版本的交换操作尽管可能更少，但是数据元素往往相距很远，缓存机制几乎完全失效。

字宽

对任意整数，求2^n

蛮力迭代版

__int64 power2BF_I ( int n ) { //幂函数2^n算法（蛮力迭代版），n >= 0
   __int64 pow = 1; //O(1)：累积器初始化为2^0
   while ( 0 < n -- ) //O(n)：迭代n轮，每轮都
      pow <<= 1; //O(1)：将累积器翻倍
   return pow; //O(1)：返回累积器
} //O(n) = O(2^r)，r为输入指数n的比特位数

优化迭代版

__int64 power2_I ( int n ) { //幂函数2^n算法（优化迭代版），n >= 0
   __int64 pow = 1; //O(1)：累积器初始化为2^0
   __int64 p = 2; //O(1)：累乘项初始化为2
   while ( 0 < n ) { //O(logn)：迭代log(n)轮，每轮都
      if ( n & 1 ) //O(1)：根据当前比特位是否为1，决定是否
         pow *= p; //O(1)：将当前累乘项计入累积器
      n >>= 1; //O(1)：指数减半
      p *= p; //O(1)：累乘项自乘
   }
   return pow; //O(1)：返回累积器
} //O(logn) = O(r)，r为输入指数n的比特位数

蛮力递归版

1
2
3

__int64 power2BF ( int n ) { 
   return ( 1 > n ) ? 1 : power2BF ( n - 1 ) << 1; //递归
} //O(n) = O(2^r)，r为输入指数n的比特位数

优化递归版

inline __int64 sqr ( __int64 a ) { return a * a; }
__int64 power2 ( int n ) { //幂函数2^n算法（优化递归版），n >= 0
   if ( 0 == n ) return 1; //递归基；否则，视n的奇偶分别递归
   return ( n & 1 ) ? sqr ( power2 ( n >> 1 ) ) << 1 : sqr ( power2 ( n >> 1 ) );
} //O(logn) = O(r)，r为输入指数n的比特位数

对任何给定的整数n>0,计算$a^n$

__int64 power ( __int64 a, int n ) { //a^n算法：n >= 0
   __int64 pow = 1; //O(1)
   __int64 p = a; //O(1)
   while ( 0 < n ) { //O(logn)
      if ( n & 1 ) //O(1)
         pow *= p; //O(1)
      n >>= 1; //O(1)
      p *= p; //O(1)
   }
   return pow; //O(1)
} //power()

输入规模=n的二进制位数=r,复杂度主要取决于循环次数

$T(r)=1+1+4r+1=O(r)$

直接打印power(n)至少需要n单位的时间，而以上算法为O(logn)，存在悖论？

基于power的分析都假定，整数的除法，打印等基本操作只需要O(1)时间，即采用所谓的常数代价准则。

设参与运算的整数数值为k，上述操作都需要逐个读取K的二进制展开的每一比特位，线性正比于k的有效位的总数目，即采用所谓的对数代价准则。

随机数

随机数并不等概率地生成随机序列，随机数仍是人为制造地有规律的序列，所以无法满足随机均匀分布的假定条件。