给定一个初始值全为$0$的数列$a_1,a_2,..,a_n$
- 给定$i$,计算$a_1+a_2+…+a_n$
- 给定$i$和$x$,计算$a_i+=x$
树状数组可以在$O(logn)$时间内计算区间前缀和,在$O(logn)$时间内更新单点的值。
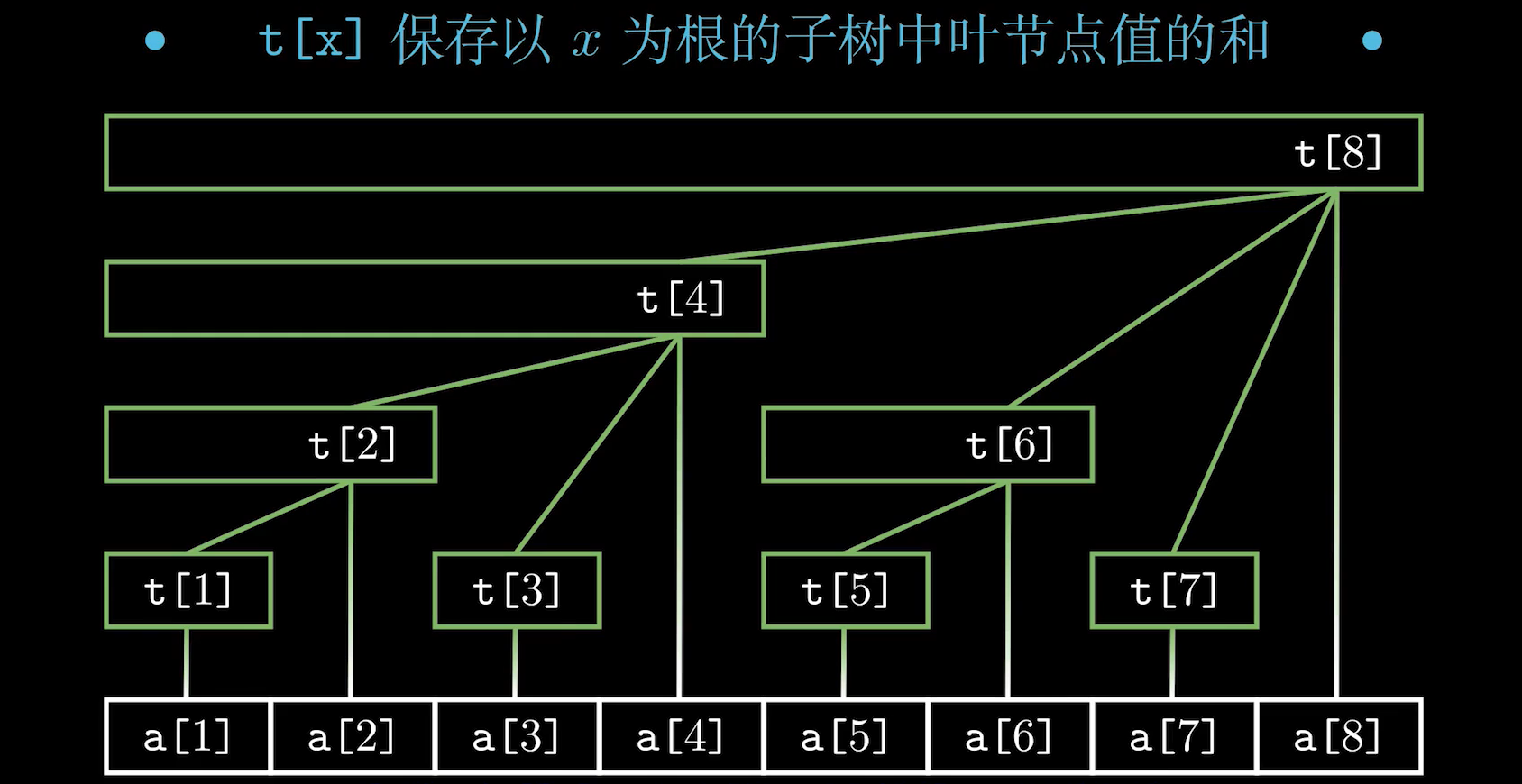
树状数组的关系图为
lowbit操作
lowbit操作返回$x$在二进制表示下为1的最低位对应的幂,例如$lowbit((101000)_2)$为$(1000)_2$。
1
2
3
| int lowbit(int x) {
return x & (-x);
}
|
lowbit求解原理为:将$x$按位取反再加一后与之前的$x$相与
例如$(101000)_2$
- 按位取反得到$(010111)_2$
- +1,得到$(011000)_2$
- $011000 &101000$,得到$ (1000)_2$
树状数组中的元素满足$t[x]=\sum_{i=x-lowbit(x)+1}^{x}a[i]$,即其中第$x$位元素的值为$x$与$lowbit(x)$之间元素的和,lowbit(x)等于当前位置所覆盖的区间长度。
单点修改和区间查询
树状数组中求前缀和和更新值的操作如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int t[maxn],n;
int sum(int i){
int res=0;
while(i>0){
res+=t[i];
i-=lowbit(i);
}
return res;
}
void add(int i,int x){
while(i<=n){
t[i]+=x;
i+=lowbit(i);
}
}
|
单点修改
每个节点的父亲都可以表示为$x+lowbit(x)$,在更新$a[x]$的时候,逐步更新其祖先节点的值。
区间查询
1
2
3
| int query(int l,int r){
return sum(r)-sum(l-1);
}
|
查询某个区间的区间和通过前缀和相减来实现,例如,求$[l,r]$的区间和,只需求$\sum_{i=1}^{r}a[i]-\sum_{i=1}^{l-1}a[i]$ 。根据lowbit(x)的性质,可以将$[1,x]$分解为一个个不相交的子区间,将各个子区间的和相加即是$[1,x]$的前缀和。
例如POJ 1990
给定$n$头牛的坐标,每头牛听力为$v_i$,两头牛($i$和$j$)之间必须以$max(v_i,v_j)$的音量沟通,沟通过程中消耗能量为$max(v_i,v_j)|x_i-x_j|$,求这$n$头牛两两沟通总共消耗多少能量。
任意两头牛之间以$max(v_i,v_j)$沟通,可以按照听力排序,从小到大处理$n$头牛。
对于正在处理的牛$i$,与其沟通所消耗的能量应该是其听力与所有听力小于该牛的坐标值之和的乘积。
维护两个树状数组,其中$bit0$用于计数,$bit1$用于计算坐标和。
维护处理过的所有牛的坐标和$tot$,并执行$add(bit0,x,1)$和$add(bit1,x,x)$。
对于牛$i$来说,
左边牛的坐标差值和为$sum(bit0,x[i])*x[i]-sum(bit1,x[i])$
右边牛的坐标差值和为$ tot-sum(bit1,x)-x[i] (i+1-sum(bit0,x[i]))$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=20005;
ll bit0[maxn],bit1[maxn];
struct Node
{
int v,x;
};
Node a[maxn];
bool cmp(Node a,Node b)
{
return a.v<b.v;
}
ll sum(ll *b,int i){
ll s=0;
while(i>0){
s+=b[i];
i-=i&(-i);
}
return s;
}
void add(ll *b,int i,int v){
while(i<maxn){
b[i]+=v;
i+=i&(-i);
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d%d",&a[i].v,&a[i].x);
}
sort(a,a+n,cmp);
ll tot=0,ans=0;
memset(bit0,0,sizeof(bit0));
memset(bit1,0,sizeof(bit1));
for(int i=0;i<n;i++){
int x=a[i].x;
tot+=x;
add(bit0,x,1);
add(bit1,x,x);
ll s1=sum(bit0,x);
ll s2=sum(bit1,x);
ll temp1=s1*x-s2;
ll temp2=tot-s2-x*(i+1-s1);
ans+=(temp1+temp2)*a[i].v;
}
printf("%lld\n",ans);
}
|
POJ 3109
先离散化所有黑棋的纵坐标,扫描线按照横坐标从左到右依次扫描,通过树状数组动态求和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #include<cstdio>
#include<vector>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=100005;
const int inf=0x3f3f3f3f;
typedef long long ll;
struct Node{
int x,y;
};
Node a[maxn];
bool cmp(Node a,Node b){
if(a.x==b.x) return a.y<a.y;
return a.x<b.x;
}
int bit[maxn];
int l[maxn],r[maxn];
int lowbit(int x){
return x&(-x);
}
int sum(int i)
{
int res=0;
while(i)
{
res+=bit[i];
i-=lowbit(i);
}
return res;
}
void add(int i,int x)
{
while(i<maxn)
{
bit[i]+= x;
i+=lowbit(i);
}
}
int main()
{
int n;
scanf("%d",&n);
vector<int> h;
for(int i=0;i<n;i++){
scanf("%d%d",&a[i].x,&a[i].y);
h.push_back(a[i].y);
}
sort(a,a+n,cmp);
sort(h.begin(),h.end());
h.erase(unique(h.begin(), h.end()), h.end());
for(int i=0;i<n;i++){
a[i].y=lower_bound(h.begin(),h.end(),a[i].y)-h.begin()+1;
}
memset(l,inf,sizeof(l));
memset(r,-inf,sizeof(r));
for(int i=0;i<n;i++){
if(l[a[i].y]==inf) l[a[i].y]=a[i].x;
r[a[i].y]=a[i].x;
}
int cnt=0;
ll ans=0;
int i=0;
while(i<n)
{
int x = a[i].x, L = inf, R = -inf;
int j = i;
while(i<n&&a[i].x == x)
{
L=min(L, a[i].y);
R=max(R, a[i].y);
if(x==l[a[i].y])
add(a[i].y, 1);
i++;
}
ans+=sum(R)-sum(L - 1);
while(j<i)
{
if(x==r[a[j].y])
add(a[j].y, -1);
j++;
}
}
printf("%lld\n",ans);
return 0;
}
|
区间修改和单点查询
为了便于执行单点查询操作,引入差分数组的概念,差分数组中$p[i]=a[i]-a[i-1]$。
$\sum_{i=1}^{x}=a[1]+(a[2]-a[1])+(a[3]-a[2])+(a[4]-a[3])+…(a[x-1]+a[x-2])+(a[x]-a[x-1])$
显然,差分数组的前缀和即是单点查询所返回的值。
这样一来,树状数组在$O(logn)$时间内求前缀和的性质可以应用于求差分数组得前缀和,从而在$O(logn)$时间内执行单点查询操作。
若想对区间$[l,r]$中所有元素同时加上$x$,同样通过差分思想来操作。差分数组维护相邻两项的差值,所以仅仅区间首尾两项会更新,其余部分的差值不变。更新时,对$p[l]+x$,$p[r+1]-x$,通过两次单点更新操作实现区间修改。
例如POJ 2155
二维树状数组的区间修改和单点查询问题,思想与一维类似,更新点由两个变为四个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=1005;
int bit[maxn][maxn];
int lowbit(int x){
return x&(-x);
}
ll sum(int x,int y){
ll s=0;
for(int i=x;i>0;i-=lowbit(i)){
for(int j=y;j>0;j-=lowbit(j)){
s+=bit[i][j];
}
}
return s;
}
void add(int x,int y,int val){
for(int i=x;i<maxn;i+=lowbit(i)){
for(int j=y;j<maxn;j+=lowbit(j)){
bit[i][j]+=val;
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--){
int n,m;
scanf("%d%d",&n,&m);
memset(bit,0,sizeof(bit));
while(m--){
char str[10];
scanf("%s",str);
if(str[0]=='C'){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
add(x1,y1,1);
add(x2+1,y1,-1);
add(x1,y2+1,-1);
add(x2+1,y2+1,1);
}
else{
int x,y;
scanf("%d%d",&x,&y);
ll ans=sum(x,y);
printf("%d\n",ans&1);
}
}
printf("\n");
}
}
|
区间修改和区间查询
区间修改和区间查询同样应用了差分思想,考虑前缀和$sum(x)=\sum_{i=1}^{x}a[i]=\sum_{i=1}^{x}\sum_{j=1}^{i}p[j]$
同时给区间$[l,r]$同时加上$x$时,树状数组中的值将会如何变化呢?
- $i<l$,$sum’(i)=sum(i)$
- $l\leq i \leq r$ ,$sum’(i)=sum(i)+x(i-l+1)=sum(i)+xi-x(l-1)$
- $r<i$,$sum’(i)=sum(i)+x(r-l+1)$
构建两个树状数组$bit0$和$bit1$,$sum(bit,i)$为树状数组的前$i$项和
$\sum_{j=1}^{i}=sum(bit1,i)i+sum(bit0,i)$
那么在$[l,r]$区间同时加上$x$就等效于
- 在$bit0$的$l$位置上加上$-x(l-1)$
- 在$bit1$的l位置上加上$x$
- 在$bit0$的位置上加上$xr$
- 在$bit1$的位置上加上$-x$
因此,区间查询和区间更新操作均可在$O(logn)$时间内完成。
例如POJ 3468
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;
int n,q;
int a[maxn];
char c[5];
int l,r,x;
ll bit0[maxn],bit1[maxn];
ll sum(ll *b,int i){
ll s=0;
while(i>0){
s+=b[i];
i-=i&-i;
}
return s;
}
void add(ll *b,int i,int v){
while(i<=n){
b[i]+=v;
i+=i&-i;
}
}
int main()
{
while(scanf("%d%d",&n,&q)==2)
{
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
add(bit0,i,a[i]);
}
for(int i=0;i<q;i++){
scanf("%s",c);
if(c[0]=='C'){
scanf("%d%d%d",&l,&r,&x);
add(bit0,l,-x*(l-1));
add(bit1,l,x);
add(bit0,r+1,x*r);
add(bit1,r+1,-x);
}
else{
scanf("%d%d",&l,&r);
ll res=0;
res+=sum(bit0,r)+sum(bit1,r)*r;
res-=sum(bit0,l-1)+sum(bit1,l-1)*(l-1);
printf("%lld\n",res);
}
}
}
return 0;
}
|
